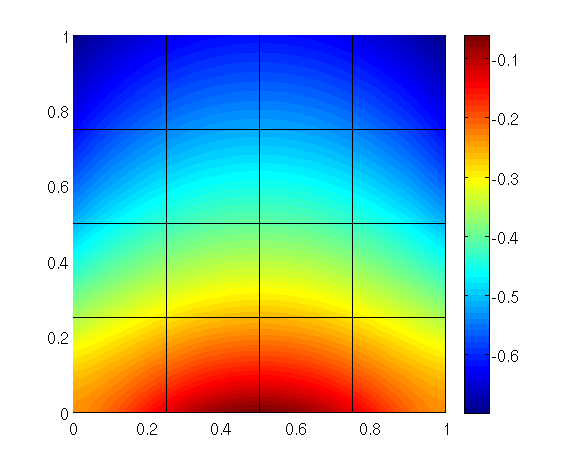
In this tutorial the implementation of Robin boundary conditions using trace spaces is shown.
Now we derive the corresponding variational formulation of the introduced problem: find
The mesh is read from three files containing the coordinates, the elements and the boundary attributes of the mesh.
In our example, the edges are given the following attributes: 1 (bottom), 2 (right), 3 (top) and 4 (left).
If there is an error reading those files, then an exception error message is returned.
else, the mesh is plotted using scaling factor of 100, a greyscale of 1.0 and one point per edge.
Since, we do not have any homogeneous Dirichlet boundary conditions we do not need to set them using bc = concepts.BoundaryConditions() .
and a set of unsigned intergers identifying the edge with attribute 1, on which the Neumann boundary condition is prescribed, is created.
Now, the same is done for the Robin data. The two formulas are defined.
and a set of unsigned intergers identifying the edge with attributes 2, 3 and 4, on which the Robin boundary condition is prescribed, is created.
In this example, there are no homogeneous Dirichlet boundary conditions and thus, the space can be built without passing any boundary data. We refine the space two times and set the polynomial degree to three. Then, the elements of the space are built and the space is plotted.
The right hand side is computed. In our case, the vector rhs only contains the integrals of the Neumann and Robin trace as the source term is zero.
Furthermore, the integrals of the Robin trace are added.
We solve the equation using a Mumps solver.
Mesh: Import2dMesh(ncell = 1)
Mesh:
Import2dMesh(ncell = 1)
RHS Vector:
Vector(169, [ 1.549354e-02, 1.678744e-01, 0.000000e+00, -9.444769e-02, 1.570060e-02, 5.980456e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -8.097468e-03, -3.200783e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 2.374103e-01, 0.000000e+00, 3.790460e-02, 2.477186e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -1.745166e-01, 0.000000e+00, 0.000000e+00, -2.305964e-02, -2.713493e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.678744e-01, 0.000000e+00, 3.790460e-02, -2.477186e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.549354e-02, -9.444769e-02, 1.570060e-02, -5.980456e-03, -8.097468e-03, -3.200783e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -1.745166e-01, 0.000000e+00, -2.305964e-02, -2.713493e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.280169e-01, -3.451119e-02, -1.813098e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.484019e-01, -2.500000e-01, -4.070872e-02, -6.366754e-04, -4.166667e-02, 1.734723e-18, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.500000e-01, -4.166667e-02, 1.734723e-18, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.280169e-01, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -3.451119e-02, -1.813098e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.500000e-01, -4.166667e-02, 1.734723e-18, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00, -2.484019e-01, -4.166667e-02, 1.734723e-18, -4.070872e-02, -6.366754e-04, 0.000000e+00, 0.000000e+00, 0.000000e+00, 0.000000e+00])
System Matrix:
SparseMatrix(169x169, HashedSparseMatrix: 2825 (9.89111%) entries bound.)
Solver:
Mumps(n = 169)
Solution:
Vector(169, [-2.358621e-01, -1.292237e-01, -2.897389e-01, -3.566355e-01, -4.559817e-02, 1.946218e-02, -1.205068e-02, 1.041054e-03, 7.644850e-03, 1.495471e-03, 6.444423e-02, -1.673132e-02, 1.587023e-03, 1.516002e-02, -1.736858e-02, 2.606585e-04, -6.104195e-02, -2.594242e-01, 6.267945e-02, 3.415858e-03, -4.265729e-02, 3.939918e-03, 2.834458e-02, -1.218636e-03, -3.113952e-02, 3.437624e-03, 4.741337e-04, -5.281713e-04, -4.024244e-01, -4.285123e-01, -1.755653e-02, 8.674954e-04, 2.607856e-02, -7.279306e-06, -1.171772e-02, 3.217059e-04, -4.662949e-03, 1.143960e-03, -7.680474e-04, 4.177298e-05, -5.093568e-01, 3.010143e-02, -9.179211e-04, -1.329014e-02, -1.956168e-03, 1.487323e-02, -1.463781e-03, -2.474342e-03, 6.503121e-04, -1.292237e-01, -2.897389e-01, 6.267945e-02, -3.415858e-03, -1.205068e-02, 1.041054e-03, 2.834458e-02, -1.218636e-03, -3.113952e-02, 3.437624e-03, -4.741337e-04, 5.281713e-04, -2.358621e-01, -3.566355e-01, -4.559817e-02, -1.946218e-02, 6.444423e-02, -1.673132e-02, 7.644850e-03, 1.495471e-03, 1.587023e-03, 1.516002e-02, 1.736858e-02, -2.606585e-04, -5.093568e-01, -4.285123e-01, -1.329014e-02, -1.956168e-03, 3.010143e-02, -9.179211e-04, -1.171772e-02, 3.217059e-04, 1.487323e-02, -1.463781e-03, 2.474342e-03, -6.503121e-04, 2.607856e-02, -7.279306e-06, -4.662949e-03, 1.143960e-03, 7.680474e-04, -4.177298e-05, -5.422839e-01, -5.175787e-01, -1.233352e-02, 2.661886e-04, 2.502922e-02, 2.062011e-04, -1.092909e-02, -4.398691e-04, 1.899724e-03, 1.311650e-04, 3.106070e-04, -2.525089e-05, -6.223890e-01, -2.309497e-02, 9.162962e-05, 3.166459e-02, -1.025598e-03, 7.912876e-03, -6.024182e-05, 5.596927e-04, 5.688176e-05, -6.986325e-01, -6.372163e-01, -1.000702e-02, 2.815548e-03, 1.919949e-02, 1.072334e-03, -5.662442e-03, -7.820322e-04, 4.555847e-03, -2.151253e-03, 2.307172e-03, 1.385236e-05, -6.168261e-01, 2.056321e-02, -1.149454e-04, -4.699151e-03, -6.026103e-04, 8.769205e-04, -2.662965e-04, -8.598998e-05, -8.702793e-05, -5.422839e-01, -6.223890e-01, -1.233352e-02, 2.661886e-04, 3.166459e-02, -1.025598e-03, -2.309497e-02, 9.162962e-05, 7.912876e-03, -6.024182e-05, -5.596927e-04, -5.688176e-05, 2.502922e-02, 2.062011e-04, 1.899724e-03, 1.311650e-04, -3.106070e-04, 2.525089e-05, -6.372163e-01, 2.056321e-02, 1.149454e-04, -5.662442e-03, -7.820322e-04, 8.769205e-04, -2.662965e-04, 8.598998e-05, 8.702793e-05, -6.986325e-01, 1.919949e-02, -1.072334e-03, -1.000702e-02, 2.815548e-03, 4.555847e-03, -2.151253e-03, -2.307172e-03, -1.385236e-05])
1
2 from libconceptspy import concepts
3 from libconceptspy import graphics
4 from libconceptspy import hp1D
5 from libconceptspy import hp2D
6
7 import os
8 from sys import exit
9 from mpi4py import MPI
10
11 SOURCEDIR = os.environ['CONCEPTSPATH' ]
12
13 def main():
14 try :
16 elms = SOURCEDIR + "/applications/unitsquareElements.dat" ,
17 boundary = SOURCEDIR + "/applications/unitsquareEdges.dat"
18 )
19 print ('Mesh:' )
20 print (mesh)
21 except RuntimeError:
22 print("Mesh import error" )
23 else :
24 graphics.MeshEPS_r(msh = mesh, filename = "mesh.eps" , scale=100, greyscale=1.0, nPoints=1)
25
26
27 NeumannFormula = concepts.ParsedFormula_r(formula = "(sin(pi*x))" )
28 attrNeumann = concepts.Set_uint(1)
29
30
31 RobinFormula1 = concepts.ParsedFormula_r(formula = "(-y)" )
32 RobinFormula2 = concepts.ParsedFormula_r(formula = "(-sin(pi/2*y))" )
33 attrRobin = concepts.Set_uint(2)
34 attrRobin.insert(3)
35 attrRobin.insert(4)
36
37
38 levelOfRefinement = 2
39 polynomialDegree = 3
41 p = polynomialDegree)
42 space.rebuild()
43 graphics.MeshEPS_r(spc = space, filename = "space.eps" , scale=100, greyscale=1.0, nPoints=1)
44
45
48
49
50 lformNeumann = hp1D.Riesz_r(frm = NeumannFormula)
51 rhsNeumann = concepts.Vector_r(spc = tscpNeumann, lf = lformNeumann)
52 lformRobin = hp1D.Riesz_r(frm = RobinFormula2)
53 rhsRobin = concepts.Vector_r(spc = tscpRobin, lf = lformRobin)
54 rhs = concepts.Vector_r()
55 rhs = rhsNeumann + rhsRobin;
56
57 print('\nRHS Vector:' )
58 print(rhs)
59
60
61
62 la = hp2D.Laplace_r()
63 A = concepts.SparseMatrix_r(spc = space, bf = la)
64 A.compress()
65
66 id = hp2D.Identity_r()
67 M = concepts.SparseMatrix_r(spc = space, bf = id)
68 M.compress()
69 M.addInto(A, 1.0)
70
71 bilformRobin = hp1D.Identity_r(frm = RobinFormula1)
72 M1D = concepts.SparseMatrix_r(spc = tscpRobin, bf = bilformRobin)
73 M1D.compress()
74 M1D.addInto(A, -1.0)
75
76 print('\nSystem Matrix:' )
77 print(A)
78
79
80 solver = concepts.Mumps_r(A = A)
81 sol = concepts.Vector_r(spc = space)
82 solver(fncY = rhs, fncX = sol)
83 print('\nSolver:' )
84 print(solver)
85 print('\nSolution:' )
86 print(sol)
87
88
89 hp2D.IntegrableQuad.setTensor(concepts.TRAPEZE, True , 8 )
90 space.recomputeShapefunctions()
92
93 if __name__ == '__main__' :
94 main()
![\[ - \Delta u + u = 0 \]](form_185.png)
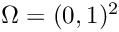
![\[
\nabla u\cdot \underline{n} = g(x,y), \qquad (x,y)\in\Gamma_{\rm N}=\{(x,y)\in\partial\Omega\mid y=0\},
\]](form_745.png)
![\[
\nabla u\cdot \underline{n} = h_1(x,y) u + h_2(x,y), \qquad (x,y)\in\Gamma_{\rm R}=\partial\Omega\setminus\Gamma_{\rm N}
\]](form_748.png)
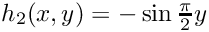
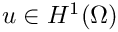
![\[
\int_{\Omega} \nabla u \cdot \nabla v \;{\rm d}x
+ \int_{\Omega} u v \;{\rm d}x
- \int_{\Gamma_{\rm R}} h_1 u v \;{\rm d}x
=
\int_{\Gamma_{\rm N}} g v \;{\rm d}x
+ \int_{\Gamma_{\rm R}} h_2 v \;{\rm d}x
\qquad\forall v\in H^1(\Omega).
\]](form_749.png)