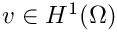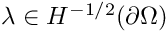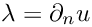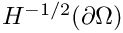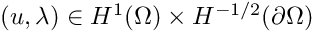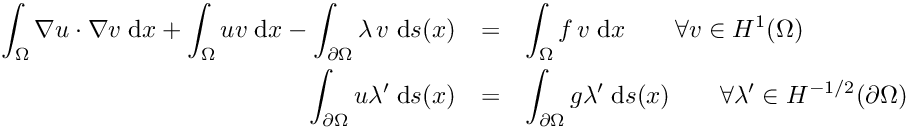In this tutorial the implementation of inhomogeneous Dirichlet boundary conditions using Lagrangian multipliers is shown.
The mesh is read from three files containing the coordinates, the elements and the boundary attributes of the mesh.
In our example, the edges are given the following attributes: 1 (bottom), 2 (right), 3 (top) and 4 (left).
If there is an error reading those files, then an exception error message is returned.
else, the mesh is plotted using scaling factor of 100, a greyscale of 1.0 and one point per edge.
The space is built using the mesh, a refinement factor of 2 and a polynomial degree to 3. Then the elements of the space are built and the space is plotted.
The right hand side is computed. First we calculate the vector corresponding to the linear form of the source term
then the vector that corresponds to the inhomogeneous Dirichlet boundary condition is built
and finally, these two vectors are put together in a block vector.
The system matrix is also assembled as a block matrix. First we account for the bilinear forms hp2D.Laplace_r and hp2D.Identity_r that build the upper right block.
We solve the equation using a Mumps solver.
Mesh: Import2dMesh(ncell = 1)
Space:
hpAdaptiveSpaceH1(dim = 169 (V:25, E:80, I:64), nelm = 16)
Trace Space:
TraceSpace(QuadEdgeFirst(EdgeNormalVectorRule()), dim = 169, nelm = 16)
Dual Space:
DualSpace(dim = 48, nelm = 16)
RHS Vector 2D:
Vector(169, [-5.494815e-02, -1.219900e-01, -2.708292e-01, -1.219900e-01, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -4.203145e-02, -1.570171e-03, -1.893229e-02, -7.072544e-04, -6.523089e-03, -2.436833e-04, -2.436833e-04, -9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, -9.199187e-05, -3.436544e-06, -3.061031e-01, -2.879265e-01, -5.059520e-02, -6.301685e-04, -5.059520e-02, -6.301685e-04, -4.759082e-02, 5.927486e-04, -8.362783e-03, -1.041593e-04, -1.041593e-04, -1.297316e-06, -1.296912e-01, -4.468487e-02, -1.669295e-03, -2.143641e-02, -2.669927e-04, -7.385877e-03, -9.199187e-05, -2.759145e-04, -3.436544e-06, -1.219900e-01, -2.708292e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, 9.199187e-05, 3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, -2.436833e-04, 2.436833e-04, 9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -9.199187e-05, 2.759145e-04, 3.436544e-06, -5.059520e-02, -6.301685e-04, -8.362783e-03, -1.041593e-04, 1.041593e-04, 1.297316e-06, -2.708292e-01, -2.879265e-01, -4.759082e-02, 5.927486e-04, -4.759082e-02, 5.927486e-04, -5.059520e-02, -6.301685e-04, -8.362783e-03, 1.041593e-04, 1.041593e-04, -1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 9.199187e-05, 2.759145e-04, -3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, 2.436833e-04, 2.436833e-04, -9.103287e-06, -1.296912e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -7.385877e-03, 2.759145e-04, 9.199187e-05, -3.436544e-06, -2.708292e-01, -1.219900e-01, -4.759082e-02, 5.927486e-04, -4.203145e-02, -1.570171e-03, -2.143641e-02, 2.669927e-04, -7.385877e-03, 9.199187e-05, -2.759145e-04, 3.436544e-06, -4.759082e-02, 5.927486e-04, -8.362783e-03, 1.041593e-04, -1.041593e-04, 1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 2.759145e-04, -9.199187e-05, 3.436544e-06, -5.494815e-02, -1.893229e-02, 7.072544e-04, -1.893229e-02, 7.072544e-04, -6.523089e-03, 2.436833e-04, -2.436833e-04, 9.103287e-06])
RHS Vector 1D:
Vector(48, [ 1.960099e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, -9.727886e-04, -1.320752e-04, 2.620727e-01, -2.348519e-03, -5.470734e-05, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, -2.348519e-03, 5.470734e-05, 1.960099e-03, 2.864357e-17, -7.696566e-20, 4.296913e-22, -9.727886e-04, 1.320752e-04, 2.192284e-17, -6.524834e-20, 1.223657e-21, 1.186456e-17, -4.359754e-20, 1.831332e-21, 1.506967e-19, 1.134717e-17, -5.956612e-20, -8.087273e-21, -1.530942e-20, 2.160204e-21, 1.604733e-17, -1.438053e-19, -3.349858e-21, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.134717e-17, -1.438053e-19, 3.349858e-21, 1.200215e-19, 0.000000e+00, 0.000000e+00, -5.956612e-20, 8.087273e-21])
RHS Vector:
Vector(217, [-5.494815e-02, -1.219900e-01, -2.708292e-01, -1.219900e-01, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -4.203145e-02, -1.570171e-03, -1.893229e-02, -7.072544e-04, -6.523089e-03, -2.436833e-04, -2.436833e-04, -9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, -9.199187e-05, -3.436544e-06, -3.061031e-01, -2.879265e-01, -5.059520e-02, -6.301685e-04, -5.059520e-02, -6.301685e-04, -4.759082e-02, 5.927486e-04, -8.362783e-03, -1.041593e-04, -1.041593e-04, -1.297316e-06, -1.296912e-01, -4.468487e-02, -1.669295e-03, -2.143641e-02, -2.669927e-04, -7.385877e-03, -9.199187e-05, -2.759145e-04, -3.436544e-06, -1.219900e-01, -2.708292e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -2.759145e-04, 9.199187e-05, 3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, -2.436833e-04, 2.436833e-04, 9.103287e-06, -1.296912e-01, -2.879265e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -4.759082e-02, 5.927486e-04, -7.385877e-03, -9.199187e-05, 2.759145e-04, 3.436544e-06, -5.059520e-02, -6.301685e-04, -8.362783e-03, -1.041593e-04, 1.041593e-04, 1.297316e-06, -2.708292e-01, -2.879265e-01, -4.759082e-02, 5.927486e-04, -4.759082e-02, 5.927486e-04, -5.059520e-02, -6.301685e-04, -8.362783e-03, 1.041593e-04, 1.041593e-04, -1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 9.199187e-05, 2.759145e-04, -3.436544e-06, -5.494815e-02, -1.219900e-01, -1.893229e-02, 7.072544e-04, -1.893229e-02, -7.072544e-04, -4.203145e-02, -1.570171e-03, -6.523089e-03, 2.436833e-04, 2.436833e-04, -9.103287e-06, -1.296912e-01, -2.143641e-02, -2.669927e-04, -4.468487e-02, -1.669295e-03, -7.385877e-03, 2.759145e-04, 9.199187e-05, -3.436544e-06, -2.708292e-01, -1.219900e-01, -4.759082e-02, 5.927486e-04, -4.203145e-02, -1.570171e-03, -2.143641e-02, 2.669927e-04, -7.385877e-03, 9.199187e-05, -2.759145e-04, 3.436544e-06, -4.759082e-02, 5.927486e-04, -8.362783e-03, 1.041593e-04, -1.041593e-04, 1.297316e-06, -1.219900e-01, -2.143641e-02, 2.669927e-04, -4.203145e-02, -1.570171e-03, -7.385877e-03, 2.759145e-04, -9.199187e-05, 3.436544e-06, -5.494815e-02, -1.893229e-02, 7.072544e-04, -1.893229e-02, 7.072544e-04, -6.523089e-03, 2.436833e-04, -2.436833e-04, 9.103287e-06, 1.960099e-03, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, -9.727886e-04, -1.320752e-04, 2.620727e-01, -2.348519e-03, -5.470734e-05, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.853134e-01, -2.348519e-03, 5.470734e-05, 1.960099e-03, 2.864357e-17, -7.696566e-20, 4.296913e-22, -9.727886e-04, 1.320752e-04, 2.192284e-17, -6.524834e-20, 1.223657e-21, 1.186456e-17, -4.359754e-20, 1.831332e-21, 1.506967e-19, 1.134717e-17, -5.956612e-20, -8.087273e-21, -1.530942e-20, 2.160204e-21, 1.604733e-17, -1.438053e-19, -3.349858e-21, 0.000000e+00, 0.000000e+00, 0.000000e+00, 1.134717e-17, -1.438053e-19, 3.349858e-21, 1.200215e-19, 0.000000e+00, 0.000000e+00, -5.956612e-20, 8.087273e-21])
System Matrix A11:
SparseMatrix(169x169, HashedSparseMatrix: 1785 (6.24978%) entries bound.)
System Matrix M11:
SparseMatrix(169x169, HashedSparseMatrix: 2809 (9.83509%) entries bound.)
System Matrix M12:
SparseMatrix(169x169, HashedSparseMatrix: 2809 (9.83509%) entries bound.)
System Matrix M21:
SparseMatrix(48x169, HashedSparseMatrix: 112 (1.38067%) entries bound.)
System Matrix A:
SparseMatrix(217x217, HashedSparseMatrix: 3033 (6.44099%) entries bound.)
Solver:
Mumps(n = 217)
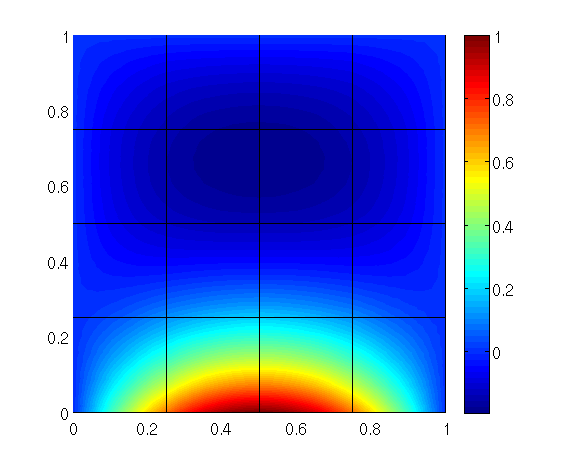
Solution u:
Vector(169, [-3.843730e-05, 7.069574e-01, 1.145216e-01, 2.745231e-17, 1.167346e-01, 1.849053e-02, -2.470302e-01, 1.513115e-02, -3.521483e-02, 1.222784e-02, -1.767987e-16, -1.300331e-16, -1.010858e-01, 1.657205e-02, 9.822506e-03, -6.715120e-03, 9.997888e-01, 1.865335e-01, 2.818223e-01, 7.659027e-03, -3.290883e-01, 1.852945e-02, 6.508946e-02, -4.285731e-03, -8.302083e-02, 4.354588e-03, -1.070311e-03, 3.682207e-04, -1.390846e-01, -1.183699e-01, -1.754996e-01, 7.990479e-03, -2.459961e-02, 2.422382e-03, -1.271322e-01, -5.897441e-03, -4.730355e-02, 2.067389e-03, -6.100085e-04, -3.252949e-05, 8.392560e-18, -7.963128e-02, 6.484164e-03, -6.632734e-17, -6.022298e-17, -2.783892e-02, 1.551738e-03, -3.120827e-03, 2.829607e-04, 7.069574e-01, 1.145216e-01, 2.818223e-01, -7.659027e-03, -2.470302e-01, 1.513115e-02, 6.508946e-02, -4.285731e-03, -8.302083e-02, 4.354588e-03, 1.070311e-03, -3.682207e-04, -3.843730e-05, 1.337389e-16, 1.167346e-01, -1.849053e-02, -2.204895e-17, -2.867429e-17, -3.521483e-02, 1.222784e-02, -1.010858e-01, 1.657205e-02, -9.822506e-03, 6.715120e-03, 9.411970e-17, -1.183699e-01, -1.148842e-16, 7.434135e-17, -7.963128e-02, 6.484164e-03, -1.271322e-01, -5.897441e-03, -2.783892e-02, 1.551738e-03, 3.120827e-03, -2.829607e-04, -2.459961e-02, 2.422382e-03, -4.730355e-02, 2.067389e-03, 6.100085e-04, 3.252949e-05, -1.455747e-01, -1.813021e-01, -8.576168e-02, 1.351167e-03, -3.808912e-02, -1.479664e-03, -1.169903e-01, -2.261285e-03, -3.094120e-02, 7.818221e-04, 1.733609e-04, -1.052648e-04, 5.297275e-17, 4.508856e-17, -3.546363e-17, -7.793839e-02, 5.447318e-03, -2.107821e-02, -3.758636e-04, 2.052405e-03, 1.006130e-04, -3.516085e-17, 4.849705e-17, -6.076754e-18, -6.568048e-18, -9.181996e-18, 5.938771e-18, -9.353945e-02, 2.845041e-03, -7.477510e-02, -1.400772e-02, -1.402845e-02, -7.228221e-03, 6.720056e-17, -1.363958e-19, 1.186490e-17, -1.120372e-01, 1.162147e-03, -1.943362e-02, 1.840870e-03, -6.726377e-04, 1.466294e-04, -1.455747e-01, -7.018279e-18, -8.576168e-02, 1.351167e-03, -7.793839e-02, 5.447318e-03, 7.994743e-17, -2.645529e-18, -2.107821e-02, -3.758636e-04, -2.052405e-03, -1.006130e-04, -3.808912e-02, -1.479664e-03, -3.094120e-02, 7.818221e-04, -1.733609e-04, 1.052648e-04, 4.682683e-17, -1.640647e-17, 1.921618e-17, -9.353945e-02, 2.845041e-03, -1.943362e-02, 1.840870e-03, 6.726377e-04, -1.466294e-04, 3.588635e-17, 2.192255e-18, -4.324464e-18, 2.505082e-17, -1.383750e-17, -7.477510e-02, -1.400772e-02, 1.402845e-02, 7.228221e-03])
Lagrangian lambda:
Vector(48, [-2.599760e-01, -3.564760e-01, 5.334279e+00, -3.591746e+00, 3.312759e+00, -2.286376e+00, 8.518971e+00, 4.523683e+00, -2.194781e+00, 2.776326e+00, 7.677355e-01, -1.142425e+00, 2.714910e+00, 3.312759e+00, -2.194781e+00, -2.776326e+00, -2.599760e-01, -3.564760e-01, 5.334279e+00, -3.591746e+00, -2.286376e+00, -8.518971e+00, 7.677355e-01, -1.142425e+00, 2.714910e+00, 8.660466e-01, -7.911928e-01, 2.372638e-01, 4.703880e-01, 9.287585e-01, 2.710241e-01, 5.898491e-01, 1.557665e-01, -4.119058e-01, 1.152213e+00, -4.279965e-01, 5.506984e-01, 8.660466e-01, -7.911928e-01, 2.372638e-01, 9.287585e-01, -4.279965e-01, -5.506984e-01, 4.703880e-01, 1.557665e-01, -4.119058e-01, 2.710241e-01, -5.898491e-01])
1
2from libconceptspy import concepts
3from libconceptspy import graphics
4from libconceptspy import hp1D
5from libconceptspy import hp2D
6
7import os
8from sys import exit
9from mpi4py import MPI
10
11SOURCEDIR = os.environ['CONCEPTSPATH']
12
13def main():
14 try:
16 elms = SOURCEDIR + "/applications/unitsquareElements.dat",
17 boundary = SOURCEDIR + "/applications/unitsquareEdges.dat"
18 )
19 print ('Mesh:')
20 print (mesh)
21 except RuntimeError:
22 print("Mesh import error")
23 else:
24 graphics.MeshEPS_r(msh = mesh, filename = "mesh.eps", scale=100, greyscale=1.0, nPoints=1)
25
26 attrBoundaryEdges = concepts.Set_uint()
27 for i in range(1,5):
28 attrBoundaryEdges.insert(i)
29
30
31 levelOfRefinement = 2
32 polynomialDegree = 3
34 space.rebuild()
35 print('\nSpace:')
36 print (space)
37 graphics.MeshEPS_r(spc = space, filename = "space.eps", scale=100, greyscale=1.0, nPoints=1 )
38
39
41 print('\nTrace Space:')
42 print (TraceSpace)
43
45 print('\nDual Space:')
46 print (DualSpace)
47
48
49 lform2D = hp2D.Riesz_r(concepts.ParsedFormula_r(formula = "(-5*exp(-(x-0.5)*(x-0.5)-(y-0.5)*(y-0.5)))"))
50 rhs2D = concepts.Vector_r(spc = space, lf = lform2D)
51 print('\nRHS Vector 2D:')
52 print(rhs2D)
53
54 lform1D = hp1D.Riesz_r(concepts.ParsedFormula_r(formula = "(sin(pi*x)*cos(pi/2*y))"))
55 rhs1D = concepts.Vector_r(spc = DualSpace, lf = lform1D)
56 print('\nRHS Vector 1D:')
57 print(rhs1D)
58
59 ds_dim = DualSpace.dim()
60 spc_dim = space.dim()
61 rhs = concepts.Vector_r(spc_dim + ds_dim)
62 rhs.data()[:spc_dim] = rhs2D.data()[:spc_dim]
63 rhs.data()[spc_dim:] = rhs1D.data()[:ds_dim]
64 print('\nRHS Vector:')
65 print (rhs)
66
67
68 la = hp2D.Laplace_r()
69 A11 = concepts.SparseMatrix_r(spc = space, bf = la)
70 A11.compress();
71 print('\nSystem Matrix A11:')
72 print(A11)
73
74 id = hp2D.Identity_r()
75 M11 = concepts.SparseMatrix_r(spc = space, bf = id)
76 M11.compress()
77 print('\nSystem Matrix M11:')
78 print(M11)
79
80 id1D = hp1D.Identity_r()
81 M12 = concepts.SparseMatrix_r(spcX = TraceSpace, spcY = DualSpace, bf = id1D)
82 M12.compress()
83 print('\nSystem Matrix M12:')
84 print(M11)
85
86 M21 = concepts.SparseMatrix_r(spcX = DualSpace, spcY = TraceSpace, bf = id1D)
87 M21.compress()
88 print('\nSystem Matrix M21:')
89 print(M21)
90
91 A = concepts.SparseMatrix_r(spc_dim + ds_dim, spc_dim + ds_dim)
92 A11.addInto(A, 1.0)
93 M11.addInto(A, 1.0)
94 M12.addInto(A, -1.0, 0, spc_dim)
95 M21.addInto(A, 1.0, spc_dim, 0)
96 print('\nSystem Matrix A:')
97 print(A)
98
99
100 solver = concepts.Mumps_r(A = A)
101 sol = concepts.Vector_r(dim = spc_dim+ds_dim)
102 solver(fncY = rhs, fncX = sol)
103 print('\nSolver:')
104 print solver
105
106
107 u = concepts.Vector_r(dim = spc_dim)
108 Lambda = concepts.Vector_r(dim = ds_dim)
109 u.data()[:spc_dim] = sol.data()[:spc_dim]
110 print('\nSolution u:')
111 print(u)
112
113 Lambda.data()[:ds_dim] = sol.data()[spc_dim:]
114 print('\nLagrangian lambda:')
115 print (Lambda)
116
117
118 hp2D.IntegrableQuad.setTensor( concepts.TRAPEZE, True, 8 )
119 space.recomputeShapefunctions()
121
122if __name__ == "__main__":
123 main()
![\[ - \Delta u + u = f \]](form_723.png)
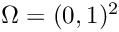
![\[
f(x,y) = -5\exp\left(-(x-1/2)^2-(y-1/2)^2\right)
\]](form_724.png)
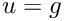
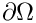
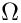
![\[
g =
\begin{cases}
\sin \pi x, &(x,y)\in\Gamma_{\rm inh}=\{(x,y)\in\partial\Omega\mid y=0\},\\
0, &(x,y)\in\partial\Omega\setminus\Gamma_{\rm inh}.
\end{cases}
\]](form_734.png)
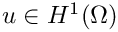
![\[
\int_{\Omega}\nabla u\cdot\nabla v\;{\rm d}x
+ \int_{\Omega} u\,v\;{\rm d}x
- \int_{\partial\Omega} \partial_n u \,v \;{\rm d}s(x)
=
\int_{\Omega} f\,v\;{\rm d}x,
\]](form_736.png)