#include <implicitResidual.hh>

Inheritance diagram for estimator::ImplicitResidual2D< F >:

Public Member Functions
	ImplicitResidual2D (const concepts::SpaceOnCells< F > &spc, const concepts::Vector< F > &sol, const concepts::ElementFormula< F > *a=0)

void	compute ()

void	addRhs (concepts::LinearForm< F > &lform, Real w=1.0)

void	addLhs (concepts::BilinearForm< F > &bform, Real w=1.0)

void	setErrorNorm (concepts::ElementFunction< F > &func, const concepts::ElementFormula< F > *w=0, Real s=1.0)

virtual const Real	operator() () const

virtual ImplicitResidual2D< F > *	clone () const

void	addBoundaryData (const concepts::Set< uint > &nSet, const concepts::ElementFormula< F > &g)

void	addBoundaryData (const concepts::Set< uint > &rSet, const concepts::ElementFormula< F > &h1, const concepts::ElementFormula< F > &h2)

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const

Protected Attributes
concepts::Sequence< const concepts::ElementFormula< F > * >	g_

concepts::Sequence< concepts::Set< uint > >	gAttrbs_

concepts::Set< uint >	eAttrbs_

Detailed Description

template<class F>
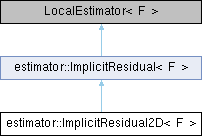
class estimator::ImplicitResidual2D< F >

Given a elliptic equation:

     Lu = f  in \Omega
    u = 0  on \Gamma_D  (Dirichletboundary)

\partial_n u = g on \Gamma_N (Neumannboundary)

Let highest order operator be given as div(alpha(x,y)*grad(.)), so consider isotropic case.

For more general case div ( IK * grad(.) ), one may think of a diffusion-tensor IK, this class is not builded up so far. MatrixFormulas will be needed. We just consider the special case IK = I*alpha so far.

Given a FEM solution u_h, the error estimator local on a element K becomes

eta_K^2 := w_K^2*||f-Lu_h||_L^2(K)^2

sum\limits_{E \subset \partial K\ w_E*||[[n^T * alpha grad u_h]]_K||_L^2(E)^2

where [[.]]_K is defined as [[.]] local on a element K where

 { [n^T * alpha grad u_h]     on inner edges E (i.e two underylying Elements)

[[v]] = { g - [n^T * alpha grad u_h] on neumann edges E (one underlying Element) { 0 on dirichlet boundary

while [.] denotes the jump and grad_n the normal derivative.

As weight w_K we may choose

w_K= diam(K)
w_K= diam(K)/(1+p_K) where p_K is minimum polynomial degree along one direction.

For weight w_E we may choose

w_E = diam(E)/2
w_E= diam(E)/2*(1+p_E) where p_E is polynomial degree along the Edge E.

The second weights are motivated from : An hp-Efficient Residual-Based A Posteriori Error Estimator for Maxwell’s Equations, Markus Bürg

and the inverse polynomial Interpolation estimates within. They may have to be taken with care for reliably error estimator, this is not checked.

We assume that all inner edges have attribute zero and no boundary edge has attribute zero.

Author: Robert Gruhlke, 2014

Definition at line 215 of file implicitResidual.hh.

Constructor & Destructor Documentation

◆ ImplicitResidual2D()

template<class F >

estimator::ImplicitResidual2D< F >::ImplicitResidual2D	(	const concepts::SpaceOnCells< F > &	spc,
		const concepts::Vector< F > &	sol,
		const concepts::ElementFormula< F > *	a = `0`
	)

inline

Constructor of the 2d implicit residual a posteriori Error estimator.

Parameters

spc	The FEM space
sol	the solution vector representing the FEM solution
wRes	The weak residual as linearform, e.g. int fv - int grad(uh) grad v for laplace
a	The coefficient function in the highest derivative operator div ( a * grad(.)) if no function `a` is given, by default `a` is const and therefore set to ONE. this is needed to define the local neumannproblems

Definition at line 234 of file implicitResidual.hh.

Member Function Documentation

◆ addBoundaryData() [1/2]

template<class F >

void estimator::ImplicitResidual< F >::addBoundaryData	(	const concepts::Set< uint > &	nSet,
		const concepts::ElementFormula< F > &	g
	)

inlineinherited

Add boundary informations (i.e. on point/edge/face) to build boundary residuals on a given requested set of edges through edge attributes.

This applicates i.e for Neumann b.c. :

Let the boundary condition be of the form :

 n^T * [A*Grad(u)] = g

Then the L2 edge residual representation has the form :

$|| g - n_e^T * [A*Grad(u_{hp})] ||_{L^2(e)}$

where n_e is the outward pointing normal vector, that comes from the underlying element that has edge e.

Definition at line 64 of file implicitResidual.hh.

◆ addBoundaryData() [2/2]

template<class F >

void estimator::ImplicitResidual< F >::addBoundaryData	(	const concepts::Set< uint > &	rSet,
		const concepts::ElementFormula< F > &	h1,
		const concepts::ElementFormula< F > &	h2
	)

inlineinherited

Add boundary informations (i.e. on point/edge/face) to build boundary residuals of the form

$h2 + h1 * u_{hp}$

on a given set of edge attributes, where u_{hp} is the trace of the hp-fem solution on the requested edges. This applicates i.e. for Robin b.c. :

Let the boundary condition be of the form :

n^T * [A*Grad(u)] = h1 * u + h2

Then the L2 edge residual representation has the form :

$|| h1 * u_{hp} + h2 - n_e^T * [A*Grad(u_{hp})] ||_{L^2(e)}$

where n_e is the outward pointing normal vector, that comes from the underlying element that has edge e.

Definition at line 98 of file implicitResidual.hh.

◆ addLhs()

template<class F >

void estimator::ImplicitResidual2D< F >::addLhs	(	concepts::BilinearForm< F > &	bform,
		Real	w = `1.0`
	)

inline

Definition at line 255 of file implicitResidual.hh.

◆ addRhs()

template<class F >

void estimator::ImplicitResidual2D< F >::addRhs	(	concepts::LinearForm< F > &	lform,
		Real	w = `1.0`
	)

inline

Definition at line 249 of file implicitResidual.hh.

◆ clone()

template<class F >

virtual ImplicitResidual2D< F > * estimator::ImplicitResidual2D< F >::clone ( ) const

inlinevirtual

Implements estimator::ImplicitResidual< F >.

Definition at line 303 of file implicitResidual.hh.

◆ compute()

template<class F >

void estimator::ImplicitResidual2D< F >::compute ( )

inline

Definition at line 244 of file implicitResidual.hh.

◆ info()

template<class F >

virtual std::ostream & estimator::ImplicitResidual2D< F >::info ( std::ostream & os ) const

inlineprotectedvirtual

Reimplemented from estimator::ImplicitResidual< F >.

Definition at line 307 of file implicitResidual.hh.

◆ operator()()

template<class F >

virtual const Real estimator::ImplicitResidual2D< F >::operator() ( ) const

inlinevirtual

Definition at line 301 of file implicitResidual.hh.

◆ setErrorNorm()

template<class F >

void estimator::ImplicitResidual2D< F >::setErrorNorm	(	concepts::ElementFunction< F > &	func,
		const concepts::ElementFormula< F > *	w = `0`,
		Real	s = `1.0`
	)

inline

Definition at line 280 of file implicitResidual.hh.

Member Data Documentation

◆ eAttrbs_

template<class F >

concepts::Set<uint> estimator::ImplicitResidual< F >::eAttrbs_

protectedinherited

Definition at line 148 of file implicitResidual.hh.

◆ g_

template<class F >

concepts::Sequence<const concepts::ElementFormula<F>* > estimator::ImplicitResidual< F >::g_

protectedinherited

Definition at line 142 of file implicitResidual.hh.

◆ gAttrbs_

template<class F >

concepts::Sequence<concepts::Set<uint> > estimator::ImplicitResidual< F >::gAttrbs_

protectedinherited

Definition at line 144 of file implicitResidual.hh.

The documentation for this class was generated from the following file:

estimator/implicitResidual.hh

Class documentation of Concepts

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

◆ ImplicitResidual2D()

Member Function Documentation

◆ addBoundaryData() [1/2]

◆ addBoundaryData() [2/2]

◆ addLhs()

◆ addRhs()

◆ clone()

◆ compute()

◆ info()

◆ operator()()

◆ setErrorNorm()

Member Data Documentation

◆ eAttrbs_

◆ g_

◆ gAttrbs_