hp1D::Neumann Class Reference

#include <linearForm.hh>

Inheritance diagram for hp1D::Neumann:

Public Member Functions
	Neumann (const concepts::BoundaryConditions *bc)
void	operator() (const concepts::Element< Real > &elm, concepts::ElementMatrix< Real > &em) const
virtual void	operator() (const Element< G > &elm, ElementMatrix< F > &em) const =0

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Protected Attributes
std::unique_ptr< BoundaryConditions >	bc_
	Reference to the boundary conditions.

Detailed Description

Linear form on edges in nD.

Point evaluation of boundary vertices which correspond to the Neumann boundary condition for one-dimensional domains.

This linear form computes

where is the data of the Neumann boundary condition.

Author

Kersten Schmidt, 2010

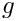
Definition at line 38 of file linearForm.hh.

Constructor & Destructor Documentation

Neumann()

hp1D::Neumann::Neumann

(

const concepts::BoundaryConditions *

bc

)

Constructor. Parses the formula.

Parameters

frm	The formula
bc	Boundary conditions, defaults to homogeneous

~Neumann()

virtual hp1D::Neumann::~Neumann ( )

virtual

Reimplemented from concepts::Neumann< Real >.

Member Function Documentation

info()

virtual std::ostream & concepts::Neumann< Real >::info ( std::ostream &  os ) const

protectedvirtualinherited

Returns information in an output stream.

Reimplemented from concepts::LinearForm< F, G >.

operator()() [1/2]

void hp1D::Neumann::operator()	(	const concepts::Element< Real > &	elm,
		concepts::ElementMatrix< Real > &	em
	)		const

Computes the element load vector. As for the computation of an element stiffness matrix, there are the loops over all quadrature points and the loops over all shape functions.

Parameters

elm	The element for which the load vector should be computed.
em	The load vector

operator()() [2/2]

template<class F , class G = typename Realtype<F>::type>

virtual void concepts::LinearForm< F, G >::operator() ( const Element< G > &  elm, ElementMatrix< F > &  em  ) const

pure virtualinherited

Computes the element contribution to the function.

Parameters

elm	Element on which the computations should be performed
em	The local matrix

Implemented in vectorial::LinearForm< F, G >.

Member Data Documentation

bc_

std::unique_ptr<BoundaryConditions> concepts::Neumann< Real >::bc_

protectedinherited

Reference to the boundary conditions.

Definition at line 100 of file linearForm.hh.

---

The documentation for this class was generated from the following file:

• hp1D/linearForm.hh