Numerical C++ Library Concepts

You are here: Concepts>Concepts Web>Class documentation

Class documentation of Concepts

Loading...

Searching...

No Matches

#include <singularSet.hh>

Public Member Functions
	SingularEdge (const concepts::Connector1 *edge, const concepts::Real3d vtx0, const concepts::Real3d vtx1)

const concepts::Connector1 *	edge () const
	Returns a pointer to the edge object (topological, connector)

Real	distance (const concepts::Real3d point, const Hexahedron *elm) const

Real	distanceV0 (const concepts::Real3d point, const Hexahedron *elm) const
	Returns the the square of the distance of `point` to `vtx0_`.

Real	distanceV1 (const concepts::Real3d point, const Hexahedron *elm) const
	Returns the the square of the distance of `point` to `vtx1_`.

Friends
std::ostream &	operator<< (std::ostream &os, const SingularEdge &s)

Detailed Description

Class for storing a singular edge with coordinates of its corners. The class also provides methods to compute a distance from a given point (in local coordinates in an element) to the edge. The returned results are the Euclidiean distance squared.

Author: Kersten Schmidt, 2002

Definition at line 30 of file singularSet.hh.

Constructor & Destructor Documentation

◆ SingularEdge()

hp3D::SingularEdge::SingularEdge	(	const concepts::Connector1 *	edge,
		const concepts::Real3d	vtx0,
		const concepts::Real3d	vtx1
	)

inline

Constructor. Precomputes diffVector_, diffVectorNormed_ and diffVectorTimesVtx0Normed_ to allow fast computations in the distance function.

Parameters

edge	Edge object
vtx0,vtx1	Coordinates of the corners of the edge

Definition at line 40 of file singularSet.hh.

Member Function Documentation

◆ distance()

Real hp3D::SingularEdge::distance	(	const concepts::Real3d	point,
		const Hexahedron *	elm
	)		const

Returns the square of the distance from the edge to a point inside elm

Parameters

point	Point in reference coordinates $\xi \in [0,1]^3$
elm	Hexahedron in which the point is located

Let 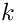be a straight line along the edge, in parameters:

$k(t) := x_c + (x_{c'}- x_c) \cdot t = x_c + x_D \cdot t$

where and $x_{c'}$ are the corners of the edge.

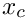
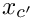
To determine the root point 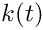of ( is $\xi$ in physical coordinates) on , compute

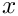
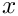
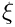
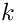
$t = x \cdot\frac{x_D}{|x_D|^2} - \frac{x_c\cdot x_D}{|x_D|^2} = x \cdot a - b$

where 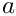= diffVectorNormed_ and 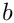= diffVectorTimesVtx0Normed_ respectively.

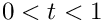
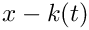
If , the closest point on the edge is not one of the corners and the distance is computed. Otherwise, the distance to the closer corner is computed.

◆ edge()

const concepts::Connector1 * hp3D::SingularEdge::edge ( ) const

inline

Returns a pointer to the edge object (topological, connector)

Definition at line 48 of file singularSet.hh.

The documentation for this class was generated from the following file:

hp3D/singularSet.hh