You are here: Concepts>Concepts Web>Class documentation

Class documentation of Concepts

Loading...
Searching...
No Matches
Public Member Functions | Protected Member Functions | List of all members
test::TestJacobian2D Class Reference

#include <testJacobian.hh>

Inheritance diagram for test::TestJacobian2D:
test::TestCase

Public Member Functions

virtual void run ()
 Runs the tests. Must be overwritten by the specialization.
 
long getNumPassed () const
 Returns number of passed tests.
 
long getNumFailed () const
 Returns number of failed tests.
 
const ostream * getStream () const
 Returns output stream.
 
void setStream (ostream *osptr)
 Sets the output stream.
 
void _succeed ()
 Explicitly succeds a test.
 
long report () const
 
virtual void reset ()
 Resets the counters for the failed and passed tests.
 

Protected Member Functions

bool do_test (bool cond, const string &lbl, const char *fname, long lineno)
 Internal function to do a test.
 
bool do_numtest (double num, double orig, const string &lbl, const string &lbl2, const char *fname, long lineno, const double tol=1e-10)
 Internal function to do a numerical test.
 
bool do_numtest (std::complex< double > num, std::complex< double > orig, const string &lbl, const string &lbl2, const char *fname, long lineno, const double tol=1e-10)
 
void do_fail (const string &lbl, const char *fname, long lineno)
 

Test routines

void testRot0Isotropic ()
 
void testRot0Horizontal ()
 
void testRot0Vertical ()
 
void testRot1Isotropic ()
 
void testRot1Horizontal ()
 
void testRot1Vertical ()
 
void testRot2Isotropic ()
 
void testRot2Horizontal ()
 
void testRot2Vertical ()
 
void testRot3Isotropic ()
 
void testRot3Horizontal ()
 
void testRot3Vertical ()
 

Detailed Description

Tests the Jacobian for anisotropic and isotropic refinements of quadrilaterals in two dimensions. The tested element map is VertexQuad2d, the tests are preformed in four different orientations.

See also
concepts::VertexQuad2d
Author
Philipp Frauenfelder, 2004

Definition at line 31 of file testJacobian.hh.

Member Function Documentation

◆ _succeed()

void test::TestCase::_succeed ( )
inlineinherited

Explicitly succeds a test.

Definition at line 112 of file testcase.hh.

◆ do_fail()

void test::TestCase::do_fail ( const string &  lbl,
const char *  fname,
long  lineno 
)
protectedinherited

Internal function to report a failed test (besides increasing the failed counter)

◆ getNumFailed()

long test::TestCase::getNumFailed ( ) const
inlineinherited

Returns number of failed tests.

Definition at line 105 of file testcase.hh.

◆ getNumPassed()

long test::TestCase::getNumPassed ( ) const
inlineinherited

Returns number of passed tests.

Definition at line 103 of file testcase.hh.

◆ getStream()

const ostream * test::TestCase::getStream ( ) const
inlineinherited

Returns output stream.

Definition at line 107 of file testcase.hh.

◆ report()

long test::TestCase::report ( ) const
inherited

Prints a report on the number of passed and failed tests to the output stream.

Returns
Number of failed tests.

◆ reset()

virtual void test::TestCase::reset ( )
inlinevirtualinherited

Resets the counters for the failed and passed tests.

Definition at line 119 of file testcase.hh.

◆ run()

virtual void test::TestJacobian2D::run ( )
virtual

Runs the tests. Must be overwritten by the specialization.

Implements test::TestCase.

◆ setStream()

void test::TestCase::setStream ( ostream *  osptr)
inlineinherited

Sets the output stream.

Definition at line 109 of file testcase.hh.

◆ testRot0Horizontal()

void test::TestJacobian2D::testRot0Horizontal ( )

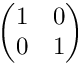
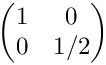
Tests Jacobians for anisotropic, horizontal subdivisions. The initial cell is (0,1)2 with the vertices (0,0), (1,0), (1,1), (0,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 1 & 0 \\ 0 & 1/2 \end{pmatrix}$

◆ testRot0Isotropic()

void test::TestJacobian2D::testRot0Isotropic ( )

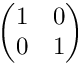
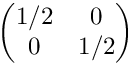
Tests Jacobians for isotropic subdivisions. The initial cell is (0,1)2 with the vertices (0,0), (1,0), (1,1), (0,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 1/2 & 0 \\ 0 & 1/2 \end{pmatrix}$

◆ testRot0Vertical()

void test::TestJacobian2D::testRot0Vertical ( )

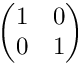
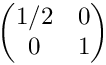
Tests Jacobians for anisotropic, vertical subdivisions. The initial cell is (0,1)2 with the vertices (0,0), (1,0), (1,1), (0,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 1/2 & 0 \\ 0 & 1 \end{pmatrix}$

◆ testRot1Horizontal()

void test::TestJacobian2D::testRot1Horizontal ( )

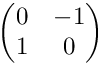
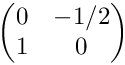
Tests Jacobians for anisotropic, horizontal subdivisions. The initial cell is (0,1)2 with the vertices (1,0), (1,1), (0,1), (0,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & -1/2 \\ 1 & 0 \end{pmatrix}$

◆ testRot1Isotropic()

void test::TestJacobian2D::testRot1Isotropic ( )

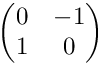
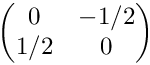
Tests Jacobians for isotropic subdivisions. The initial cell is (0,1)2 with the vertices (1,0), (1,1), (0,1), (0,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & -1/2 \\ 1/2 & 0 \end{pmatrix}$

◆ testRot1Vertical()

void test::TestJacobian2D::testRot1Vertical ( )

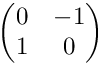
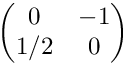
Tests Jacobians for anisotropic, vertical subdivisions. The initial cell is (0,1)2 with the vertices (1,0), (1,1), (0,1), (0,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & -1 \\ 1/2 & 0 \end{pmatrix}$

◆ testRot2Horizontal()

void test::TestJacobian2D::testRot2Horizontal ( )

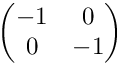
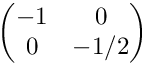
Tests Jacobians for anisotropic, horizontal subdivisions. The initial cell is (0,1)2 with the vertices (1,1), (0,1), (0,0), (1,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} -1 & 0 \\ 0 & -1/2 \end{pmatrix}$

◆ testRot2Isotropic()

void test::TestJacobian2D::testRot2Isotropic ( )

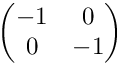
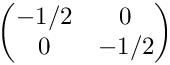
Tests Jacobians for isotropic subdivisions. The initial cell is (0,1)2 with the vertices (1,1), (0,1), (0,0), (1,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} -1/2 & 0 \\ 0 & -1/2 \end{pmatrix}$

◆ testRot2Vertical()

void test::TestJacobian2D::testRot2Vertical ( )

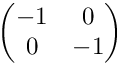
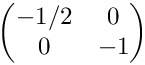
Tests Jacobians for anisotropic, vertical subdivisions. The initial cell is (0,1)2 with the vertices (1,1), (0,1), (0,0), (1,0) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}$ and one of the children has $\begin{pmatrix} -1/2 & 0 \\ 0 & -1 \end{pmatrix}$

◆ testRot3Horizontal()

void test::TestJacobian2D::testRot3Horizontal ( )

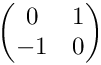
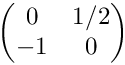
Tests Jacobians for anisotropic, horizontal subdivisions. The initial cell is (0,1)2 with the vertices (0,1), (0,0), (1,0), (1,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & 1/2 \\ -1 & 0 \end{pmatrix}$

◆ testRot3Isotropic()

void test::TestJacobian2D::testRot3Isotropic ( )

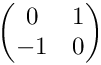
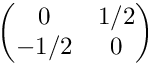
Tests Jacobians for isotropic subdivisions. The initial cell is (0,1)2 with the vertices (0,1), (0,0), (1,0), (1,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & 1/2 \\ -1/2 & 0 \end{pmatrix}$

◆ testRot3Vertical()

void test::TestJacobian2D::testRot3Vertical ( )

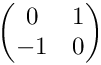
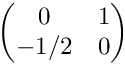
Tests Jacobians for anisotropic, vertical subdivisions. The initial cell is (0,1)2 with the vertices (0,1), (0,0), (1,0), (1,1) (in this order). The Jacobian in the initial cell is $\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ and one of the children has $\begin{pmatrix} 0 & 1 \\ -1/2 & 0 \end{pmatrix}$

The documentation for this class was generated from the following file:
Generated on Wed Sep 13 2023 21:06:59 for Concepts by doxygen 1.9.8