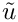Introduction Variational Formulation Commented Program Results Complete Source Code
In this tutorial the implementation of inhomogeneous Dirichlet boundary conditions using a Dirichlet lift ansatz is shown.
The equation solved is the reaction-diffusion equation
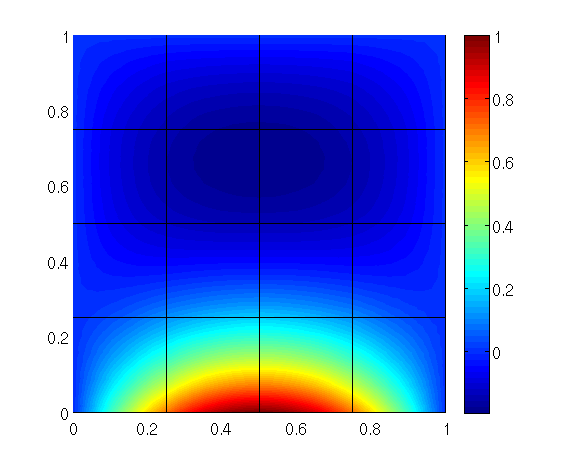
in the unit square
and Dirichlet boundary conditions
A suitable Dirichlet lift is
By setting
with homogeneous Dirichlet boundary conditions
Now we derive the corresponding variational formulation of the introduced problem: find
Commented Program
First we have to import certain modules from the libconceptspy package.
2 from libconceptspy
import concepts
3 from libconceptspy
import hp1D
4 from libconceptspy
import hp2D
5 from libconceptspy
import graphics
The module concepts contains essential functionalities and must be loaded at first. The modules hp2D graphics is used for the graphical output of the mesh and the solution.
In order to use MUMPS as a solver, we need to import MPI.
The mesh is read from three files containing the coordinates, the elements and the boundary attributes of the mesh.
18 elms = SOURCEDIR +
"/applications/unitsquareElements.dat" ,
19 boundary= SOURCEDIR +
"/applications/unitsquareEdges.dat" If there is an error reading those files, then an exception error message is returned.
25 print(
"Mesh import error" )
else, the mesh is plotted using scaling factor of 100, a greyscale of 1.0 and one point per edge.
28 graphics.MeshEPS_r(msh = mesh, filename =
"mesh.eps" , scale=100, greyscale=1.0, nPoints=1)
The Dirichlet lift and its gradient are defined.
31 DirichletLift = concepts.ParsedFormula_r(formula=
"(sin(pi*x)*cos(pi/2*y))" )
32 DirichletLiftGradx = concepts.ParsedFormula_r(formula=
"(pi*cos(pi*x)*cos(pi/2*y))" )
33 DirichletLiftGrady = concepts.ParsedFormula_r(formula=
"(-pi/2*sin(pi*x)*sin(pi/2*y))" )
The problem for
38 boundaryConditions.add(attrib = i, bcObject =
concepts.Boundary (type = concepts.Boundary.DIRICHLET))
Using the mesh and the homogeneous Dirichlet boundary conditions, the space can be built. We refine the space two times and set the polynomial degree to three. Then the elements of the space are built and the space is plotted.
45 graphics.MeshEPS_r(spc = space, filename =
"space.eps" , scale=100, greyscale=1.0, nPoints=1 )
The right hand side is computed, containing the integrals of the source term, the Dirichlet lift and its gradient.
48 lform = hp2D.Riesz_r(frm = concepts.ParsedFormula_r( formula =
"(-5*exp(-(x-0.5)*(x-0.5)-(y-0.5)*(y-0.5)))" ) )
49 rhs = concepts.Vector_r(spc = space, lf = lform)
51 lformDirichletGrad = hp2D.GradLinearForm_r(frm1=DirichletLiftGradx, frm2=DirichletLiftGrady)
52 rhsDirichletGrad = concepts.Vector_r(spc = space, lf = lformDirichletGrad)
54 lformDirichlet = hp2D.Riesz_r(frm = DirichletLift)
55 rhsDirichlet = concepts.Vector_r(spc = space, lf = lformDirichlet)
57 rhs = rhs - rhsDirichletGrad - rhsDirichlet
58 print(
'RHS Vector:\n' )
The system matrix is computed from the bilinear form hp2D.Laplace_r and the bilinear form hp2D.Identity_r.
63 A = concepts.SparseMatrix_r(spc = space, bf = la)
66 id = hp2D.Identity_r()
67 M = concepts.SparseMatrix_r(spc = space, bf = id)
70 print(
'\n System Matrix:\n' )
We solve the equation using a Mumps solver
74 solver = concepts.Mumps_r(A = A)
75 sol = concepts.Vector_r(spc = space)
76 solver(fncY = rhs, fncX = sol)
In order to add the Dirichlet lift to the solution of the homogeneous Dirichlet problem we transform the solution, that is given as a vector related to the basis functions of space, into an element formula, that can be evaluated at each point in every cell.
82 solFormula = concepts.ElementFormulaVector_1(spc = space, v = sol, f = hp2D.Value_r_r())
83 print (
'\nSolution:\n' )
84 print(concepts.ElementFormulaContainer_r_r(solFormula)+concepts.ElementFormulaContainer_r_r(DirichletLift))
We save the solutions, the homogeneous Dirichlet solution and the Dirichlet lift in a MAT-file. To this end, the shape functions are computed on equidistant points using the trapezoidal quadrature rule.
88 hp2D.IntegrableQuad.setTensor( concepts.TRAPEZE,
True , 8 )
89 space.recomputeShapefunctions()
93 filename =
"inhomDirichlet" ,
94 frm = concepts.ElementFormulaContainer_r_r(solFormula)+concepts.ElementFormulaContainer_r_r(DirichletLift))
Output of the program:
Mesh: Import2dMesh(ncell = 1)
RHS Vector:
Vector(121, [-7.813458e-01, -1.331759e-01, -1.446913e-04, -8.977796e-02, -1.975711e-02, -1.504745e-02, -1.103641e-04, -3.490666e-03, 4.167881e-05, -1.009906e+00, -1.735826e-01, 3.466376e-04, -1.628611e-01, 8.126026e-03, -2.796551e-02, 4.594644e-05, -1.436936e-03, 1.759809e-05, -8.586824e-01, -6.786590e-01, -1.598694e-01, 5.110721e-03, -1.388192e-01, -6.395889e-03, -1.248594e-01, -3.466673e-03, -2.580936e-02, 8.124231e-04, -1.244348e-03, 5.860425e-05, -8.122847e-02, -1.558898e-02, -1.461248e-02, 2.876690e-04, -3.028574e-03, 1.411786e-04, -7.813458e-01, -1.331759e-01, -1.446913e-04, -1.628611e-01, 8.126026e-03, -2.796551e-02, 4.594644e-05, 1.436936e-03, -1.759809e-05, -8.977796e-02, -1.975711e-02, -1.504745e-02, -1.103641e-04, 3.490666e-03, -4.167881e-05, -6.786590e-01, -8.122847e-02, -1.558898e-02, -1.248594e-01, -3.466673e-03, -1.461248e-02, 2.876690e-04, 3.028574e-03, -1.411786e-04, -1.388192e-01, -6.395889e-03, -2.580936e-02, 8.124231e-04, 1.244348e-03, -5.860425e-05, -4.822921e-01, -5.869802e-01, -9.922001e-02, 6.668103e-03, -9.533732e-02, 3.713134e-03, -1.236099e-01, -9.222017e-03, -2.002021e-02, 1.475922e-03, 8.660092e-04, -9.094635e-05, -6.180870e-02, -9.103448e-03, -1.221454e-02, 6.601945e-04, 2.115183e-03, -2.198685e-04, -6.016121e-02, -8.736539e-03, -8.218690e-03, 9.139240e-04, 8.895484e-04, -2.644021e-04, -7.032423e-02, -1.180407e-02, -1.147942e-02, 1.894019e-03, 3.595180e-04, -1.091848e-04, -4.822921e-01, -9.922001e-02, 6.668103e-03, -6.180870e-02, -9.103448e-03, -1.221454e-02, 6.601945e-04, -2.115183e-03, 2.198685e-04, -9.533732e-02, 3.713134e-03, -2.002021e-02, 1.475922e-03, -8.660092e-04, 9.094635e-05, -6.016121e-02, -8.736539e-03, -1.147942e-02, 1.894019e-03, -3.595180e-04, 1.091848e-04, -8.218690e-03, 9.139240e-04, -8.895484e-04, 2.644021e-04])
System Matrix:
SparseMatrix(121x121, HashedSparseMatrix: 1521 (10.3886%) entries bound.)
Solver:
Mumps(n = 121)
Solution:
FrmE_Sum(ElementFormulaVector<1>(
hp2D ::Value<
double >(), Vector(121, [-5.387654e-01, -3.006218e-01, 1.564124e-02, -1.425659e-01, -4.809499e-03, -1.088256e-01, 1.611971e-02, 8.625588e-03, -6.891406e-03, -7.373583e-01, -4.048944e-01, 1.925875e-02, -1.941122e-01, 2.767690e-03, -1.016416e-01, 3.259733e-03, -1.569518e-03, 2.857100e-04, -8.461932e-01, -6.183710e-01, -2.393483e-01, 9.380839e-03, -2.230022e-01, -2.981412e-03, -1.722831e-01, -6.882467e-03, -6.528885e-02, 2.490903e-03, -1.108972e-03, -1.050398e-05, -1.618117e-01, -6.560393e-03, -3.530271e-02, 1.727733e-03, -4.305751e-03, 3.179923e-04, -5.387655e-01, -3.006218e-01, 1.564124e-02, -1.941122e-01, 2.767687e-03, -1.016416e-01, 3.259733e-03, 1.569518e-03, -2.857100e-04, -1.425659e-01, -4.809502e-03, -1.088256e-01, 1.611971e-02, -8.625588e-03, 6.891407e-03, -6.183710e-01, -1.618117e-01, -6.560394e-03, -1.722831e-01, -6.882469e-03, -3.530271e-02, 1.727733e-03, 4.305752e-03, -3.179924e-04, -2.230022e-01, -2.981412e-03, -6.528885e-02, 2.490903e-03, 1.108972e-03, 1.050400e-05, -4.161721e-01, -5.639852e-01, -1.159405e-01, 2.828855e-03, -1.454700e-01, 1.444007e-03, -1.596678e-01, -4.353042e-03, -4.288914e-02, 1.375478e-03, 4.954845e-04, -1.172436e-04, -1.224176e-01, -1.613845e-03, -2.602445e-02, -1.262254e-04, 2.824662e-03, 6.029993e-05, -1.041387e-01, 1.097789e-03, -7.650684e-02, -1.372658e-02, -1.375732e-02, -7.269106e-03, -1.270253e-01, -1.308806e-03, -2.361722e-02, 2.517779e-03, -5.561139e-04, 1.292617e-04, -4.161721e-01, -1.159405e-01, 2.828853e-03, -1.224176e-01, -1.613847e-03, -2.602445e-02, -1.262255e-04, -2.824662e-03, -6.029997e-05, -1.454700e-01, 1.444005e-03, -4.288914e-02, 1.375478e-03, -4.954845e-04, 1.172437e-04, -1.041387e-01, 1.097788e-03, -2.361722e-02, 2.517779e-03, 5.561139e-04, -1.292618e-04, -7.650684e-02, -1.372658e-02, 1.375732e-02, 7.269106e-03])) + ParsedFormula<Real>((sin(pi*x)*cos(pi/2*y))))
Matlab plot of the solution:
@section complete Complete Source Code
1
2 from libconceptspy import concepts
3 from libconceptspy import hp1D
4 from libconceptspy import hp2D
5 from libconceptspy import graphics
6
7 import os
8 from sys import exit
9 from mpi4py import MPI
10
11 SOURCEDIR = os.environ['CONCEPTSPATH' ]
12
13 def main():
14 try :
16 elms = SOURCEDIR + "/applications/unitsquareElements.dat" ,
17 boundary= SOURCEDIR + "/applications/unitsquareEdges.dat"
18 )
19 print ('Mesh:' )
20 print (mesh)
21 except RuntimeError:
22 print("Mesh import error" )
23 else :
24 graphics.MeshEPS_r(msh = mesh, filename = "mesh.eps" , scale=100, greyscale=1.0, nPoints=1)
25
26 DirichletLift = concepts.ParsedFormula_r(formula="(sin(pi*x)*cos(pi/2*y))" )
27 DirichletLiftGradx = concepts.ParsedFormula_r(formula="(pi*cos(pi*x)*cos(pi/2*y))" )
28 DirichletLiftGrady = concepts.ParsedFormula_r(formula="(-pi/2*sin(pi*x)*sin(pi/2*y))" )
29
31 for i in range(1,5):
32 boundaryConditions.add(attrib = i, bcObject =
concepts.Boundary (type = concepts.Boundary.DIRICHLET))
33
35 space.rebuild();
36 print('\nSpace:' )
37 print (space)
38 graphics.MeshEPS_r(spc = space, filename = "space.eps" , scale=100, greyscale=1.0, nPoints=1 )
39
40 lform = hp2D.Riesz_r(frm = concepts.ParsedFormula_r( formula = "(-5*exp(-(x-0.5)*(x-0.5)-(y-0.5)*(y-0.5)))" ) )
41 rhs = concepts.Vector_r(spc = space, lf = lform)
42
43 lformDirichletGrad = hp2D.GradLinearForm_r(frm1=DirichletLiftGradx, frm2=DirichletLiftGrady)
44 rhsDirichletGrad = concepts.Vector_r(spc = space, lf = lformDirichletGrad)
45
46 lformDirichlet = hp2D.Riesz_r(frm = DirichletLift)
47 rhsDirichlet = concepts.Vector_r(spc = space, lf = lformDirichlet)
48
49 rhs = rhs - rhsDirichletGrad - rhsDirichlet
50 print('RHS Vector:\n' )
51 print(rhs)
52
53 la = hp2D.Laplace_r()
54 A = concepts.SparseMatrix_r(spc = space, bf = la)
55 A.compress()
56
57 id = hp2D.Identity_r()
58 M = concepts.SparseMatrix_r(spc = space, bf = id)
59 M.compress()
60 M.addInto(A,1.0)
61 print('\n System Matrix:\n' )
62 print(A)
63
64 solver = concepts.Mumps_r(A = A)
65 sol = concepts.Vector_r(spc = space)
66 solver(fncY = rhs, fncX = sol)
67 print('\nSolver:\n' )
68 print solver
69
70
71 solFormula = concepts.ElementFormulaVector_1(spc = space, v = sol, f = hp2D.Value_r_r())
72 print ('\nSolution:\n' )
73 print(concepts.ElementFormulaContainer_r_r(solFormula)+concepts.ElementFormulaContainer_r_r(DirichletLift))
74
75
76 hp2D.IntegrableQuad.setTensor( concepts.TRAPEZE, True , 8 )
77 space.recomputeShapefunctions()
78
79
81 filename = "inhomDirichlet" ,
82 frm = concepts.ElementFormulaContainer_r_r(solFormula)+concepts.ElementFormulaContainer_r_r(DirichletLift))
83
86
87
88 if __name__ == "__main__" :
89 main()
90
![\[ - \Delta u + u = f \]](form_723.png)
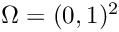
![\[
f(x,y) = -5\exp\left(-(x-1/2)^2-(y-1/2)^2\right)
\]](form_724.png)
![\[
u =
\begin{cases}
\sin \pi x, &(x,y)\in\Gamma_{\rm inh}=\{(x,y)\in\partial\Omega\mid y=0\},\\
0, &(x,y)\in\partial\Omega\setminus\Gamma_{\rm inh}.
\end{cases}
\]](form_725.png)
![\[ g = \sin \pi x \; \cos \frac{\pi}{2} y. \]](form_726.png)
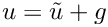
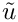
![\[
- \Delta \tilde{u} + \tilde{u} = f + \Delta g - g, \qquad x\in\Omega,
\]](form_729.png)
![\[
\tilde{u} = 0, \qquad x\in\partial\Omega.
\]](form_730.png)
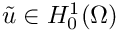
![\[
\int_{\Omega}\nabla\tilde{u}\cdot\nabla v\;{\rm d}x
+ \int_{\Omega}\tilde{u}v\;{\rm d}x
=
\int_{\Omega}fv\;{\rm d}x
-\int_{\Omega}\nabla g\cdot\nabla v\;{\rm d}x
- \int_{\Omega}gv\;{\rm d}x \qquad\forall v\in H^1_0(\Omega).
\]](form_732.png)