Namespaces
namespace	l2

Classes
class	AdaptiveModel

class	Advection

class	ApproxMoments

class	APrioriGeometricRefinement

class	APrioriRefinement

class	APrioriRefinementNew

class	APrioriRefinementRule

class	APrioriRefinementRuleFactory

class	APrioriRegularRefinement

class	ArrayElementFormula

class	ArrayQuadWeights

class	BaseEdge

class	BaseQuad

class	BaseQuadGraphics

class	BilinearFormHelper_0_0

class	BilinearFormHelper_0_1_Part

class	BilinearFormHelper_1_1

class	BilinearFormHelper_2_1

class	BilinearFormHelper_2_2

class	BilinearFormOnePartDeriv

class	BilinearFormTwoPartDeriv

class	BuildDofsBase

class	BuildEdgeDofs

class	BuildH1EdgeTColumns

class	BuildH1InnerTColumns

class	BuildH1InnerTColumnsHypTrunk

class	BuildH1InnerTColumnsLinTrunk

class	BuildH1VtxTColumns

class	BuildHCurlEdgeTColumns

class	BuildHCurlInnerTColumns

class	BuildInnerDofs

class	BuildInnerDofsHypTrunk

class	BuildInnerDofsLinTrunk

class	BuildL2InnerTColumns

class	BuildL2InnerTColumnsHypTrunk

class	BuildL2InnerTColumnsLinTrunk

class	BuildTColumnsBase

class	BuildVertexDofs

struct	DegreeDim

struct	DegreeDim< concepts::InfiniteQuad >

struct	DegreeDim< concepts::Quad >

struct	DegreeDim< concepts::Triangle >

class	DistancePost

class	DivDiv

class	Eddy2D_dissipation

class	Eddy2D_E

class	Eddy2D_eField

class	Eddy2D_H

class	Eddy2D_H_Interior

class	EdgeGraphics

class	Element

class	ElementFormulaEdgeJump

class	ElementFormulaEdgeMean

class	ElementFormulaInterpGrad

class	ElementFormulaInterpGrad< F, 2 >

class	ElementFormulaInterpGradN

class	ElementFormulaInterpGradN< F, 2 >

class	ElementFormulaSignNormalVector

class	ElementFunction

class	ElementFunction< 1, F, Q >

class	EquilibratedMomentsAO

class	Extrema

class	FormulaFromWeight

class	Grad

class	GradLinearForm

class	GridInfo

class	H1Extension

class	hpAdaptiveSpace

class	hpAdaptiveSpaceDG

class	hpAdaptiveSpaceH1

class	hpAdaptiveSpaceHCurl

class	hpAdaptiveSpaceHCurl_H1

class	hpAdaptiveSpaceL2

class	hpFull

class	Identity

class	InfiniteLaguerreQuad

class	InfiniteQuad

class	InfiniteQuadFunctions

class	InfiniteQuadGraphics

class	InputEddy2D_E

class	InputEddy2D_H

class	InputMaxwell2D_E

class	InputMaxwell2D_H

class	IntegrableQuad

class	KarniadakisDeriv2

class	Laplace

class	LaplaceBase

class	LaplaceMatrix

class	Laplacian

class	LinearFormHelper_0

class	LinearFormHelper_1

class	LinearFormHelper_2

class	LinearFormHelper_t

class	Maxwell2D_dissipation

class	Maxwell2D_E

class	Maxwell2D_eField

class	Maxwell2D_H

class	Maxwell2D_H_Base

class	Maxwell2D_H_DD

class	Maxwell2D_hField

class	MaxwellSharedData

class	NeumannTrace

class	NeumannTraceElement

class	NeumannTraceSpace

class	NotConnectedIndex

class	NTElement_BA

class	Partial_xx

class	Partial_yy

class	PlCurl

class	PlCurlLinearForm

class	PolyEdgeMax

class	PolyEdgeMin

class	PolyEdgeMinNeighMaxChild

class	PolyEdgeRule

class	Postprocess4

class	Postprocess7

class	Postprocess8

class	Postprocess9

class	PostprocessSqrt

class	Quad

class	QuadEdgeBase

class	QuadEdgeFirst

class	QuadEdgeJump

class	QuadEdgeMean

class	QuadFunctions

class	QuadGraphics

class	QuadShapeFunctions

class	RecomputeShapefct

class	Riesz

class	RotRot

class	ShapeFunction2D

class	ShortestDist

class	SingularSet

class	SingularVertex

class	Space

class	SpacePreBuilder

class	SumFactorization

class	Trace

class	TraceDeriv

class	TraceSpace

class	TransmissionWeight

class	TransmissionWeightProd

class	TrivialWeight

class	Value

Typedefs
typedef hpAdaptiveSpaceDG< hpAdaptiveSpaceH1 >	hpAdaptiveSpaceH1_DG

typedef hpAdaptiveSpaceDG< hpAdaptiveSpaceL2 >	hpAdaptiveSpaceL2_DG

typedef concepts::Adaptivity< concepts::Connector, concepts::AdaptiveAdjustP< 2 > >	Adaptivity

Enumerations
enum	partDerivType { NO_DERIV = 0 , X_DERIV = 1 , Y_DERIV = 2 }

Functions
template<class F >
void	setupAdvection (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm, bool transpose=true)

template<class F >
void	setupDivDiv (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type > frm=concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >())

template<class F >
void	setupIdDiv (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< F > frm=concepts::ElementFormulaContainer< F >())

template<class F >
void	setupIdentity (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< F > frm=concepts::ElementFormulaContainer< F >())

template<class F >
void	setupIdentity (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< concepts::Mapping< F, 2 > > frm, bool transpose=false)

template<class F >
void	setupLaplace (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type > frm=concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >())

template<class F >
void	setupLinStrainStrain (vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &bf, const concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type > frm=concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >())

hpAdaptiveSpaceH1 *	hpAdaptiveSpaceH1FromInput (concepts::Mesh2 &msh, const concepts::InOutParameters input, bool verbose=false)

hpAdaptiveSpaceH1_DG *	hpAdaptiveSpaceH1_DGFromInput (concepts::Mesh2 &msh, const concepts::InOutParameters input, bool verbose=false)

hpAdaptiveSpaceL2 *	hpAdaptiveSpaceL2FromInput (concepts::Mesh2 &msh, const concepts::InOutParameters input, bool verbose=false)

template<class F >
void	setupRiesz (vectorial::LinearForm< F, typename concepts::Realtype< F >::type > &lf, const concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm)

template<class F >
void	setupGradLinearForm (vectorial::LinearForm< F, typename concepts::Realtype< F >::type > &lf, const concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm1, const concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm2)

void	setQuadrature (enum concepts::intRule rule, uint noP)

void	refinehpFull (hp2D::hpFull &prebuild, std::string refinement)

template<class F >
ShapeFunction2D< F >	makeShapeFunction2D (const Quad< F > &quad)

std::ostream &	operator<< (std::ostream &os, const TrivialWeight &p)

std::ostream &	operator<< (std::ostream &os, const ShortestDist &p)

template<typename DistClass , typename Function >
std::ostream &	operator<< (std::ostream &os, const DistancePost< DistClass, Function > &p)

std::ostream &	operator<< (std::ostream &os, const Postprocess4 &p)

std::ostream &	operator<< (std::ostream &os, const Postprocess7 &p)

std::ostream &	operator<< (std::ostream &os, const Postprocess8 &p)

std::ostream &	operator<< (std::ostream &os, const Postprocess9 &p)

std::ostream &	operator<< (std::ostream &os, const PostprocessSqrt &p)

std::ostream &	operator<< (std::ostream &os, const TransmissionWeight &p)

std::ostream &	operator<< (std::ostream &os, const TransmissionWeightProd &p)

hpAdaptiveSpaceHCurl *	hpAdaptiveSpaceHCurlFromInput (concepts::Mesh2 &msh, const concepts::InOutParameters input, bool verbose=false)

Detailed Description

2D hp-FEM for H¹-conforming elements.

The Space can be built using full tensor product polynomial spaces in the elements or trunk spaces (and much more) by changing the way the degrees of freedom are built in the BuildDofsBase class (and its specializations).

Author: Philipp Frauenfelder, 2001

Typedef Documentation

◆ Adaptivity

typedef concepts::Adaptivity<concepts::Connector, concepts::AdaptiveAdjustP<2> > hp2D::Adaptivity

Definition at line 90 of file spacePreBuilder.hh.

◆ hpAdaptiveSpaceH1_DG

typedef hpAdaptiveSpaceDG<hpAdaptiveSpaceH1> hp2D::hpAdaptiveSpaceH1_DG

Definition at line 18 of file hpAdaptiveSpaceH1_DG.hh.

◆ hpAdaptiveSpaceL2_DG

typedef hpAdaptiveSpaceDG<hpAdaptiveSpaceL2> hp2D::hpAdaptiveSpaceL2_DG

Definition at line 17 of file hpAdaptiveSpaceL2_DG.hh.

Enumeration Type Documentation

◆ partDerivType

enum hp2D::partDerivType

Direction of partial derivative

NO_DERIV no derivative X_DERIV partial derivative in x Y_DERIV partial derivative in y

Definition at line 59 of file bf_partialderiv.hh.

Function Documentation

◆ hpAdaptiveSpaceH1_DGFromInput()

hpAdaptiveSpaceH1_DG * hp2D::hpAdaptiveSpaceH1_DGFromInput	(	concepts::Mesh2 &	msh,
		const concepts::InOutParameters	input,
		bool	verbose = `false`
	)

Builds and refines a piecewise hp-adaptive H^1-conforming space with use of input parameters.

As input parameter is needed:

"p"             - an integer value for the polynomial degrees,
"domain_Attrib" - cell attributes of the domains,
                  e.g. taking "1 2 3;4" there are two sub-domains with continuous basis
                  functions in each, where the first sub-domain consists of cells with
                  attributes 1, 2 or 3, and the second of cells with attributes 4.

There may be used the input parameters:

"refinement"       - string with refinement rules, e.g. "h1|0 in 1 -> v2".
"dirichl_bdAttrib" - string with attributes of edges with homogeneous Dirichlet boundary condition, e.g. "100; 102"


"hpAdaptiveSpace_isTrunk" - boolean indicating the use of linear trunk space or not, by default,
                            the trunk space is built.

See also: refinehpFull

Author: Kersten Schmidt, 2010

◆ hpAdaptiveSpaceH1FromInput()

hpAdaptiveSpaceH1 * hp2D::hpAdaptiveSpaceH1FromInput	(	concepts::Mesh2 &	msh,
		const concepts::InOutParameters	input,
		bool	verbose = `false`
	)

Builds and refines a hp-adaptive H^1-conforming space with use of input parameters.

As input parameter is needed:

"p" - an integer value for the polynomial degrees.

There may be used the input parameters:

"refinement"       - string with refinement rules, e.g. "h1|0 in 1 -> v2".
"dirichl_bdAttrib" - string with attributes of edges with homogeneous Dirichlet boundary condition, e.g. "100; 102"

"hpAdaptiveSpace_isTrunk" - boolean indicating the use of linear trunk space or not, by default, non trunk space is built.

See also: refinehpFull

Author: Kersten Schmidt, 2009

◆ hpAdaptiveSpaceHCurlFromInput()

hpAdaptiveSpaceHCurl * hp2D::hpAdaptiveSpaceHCurlFromInput	(	concepts::Mesh2 &	msh,
		const concepts::InOutParameters	input,
		bool	verbose = `false`
	)

Builds and refines a hp-adaptive H(curl)-conforming space with use of input parameters.

As input parameter is needed:

"p" - an integer value for the polynomial degrees.

There may be used the input parameters:

"refinement"       - string with refinement rules, e.g. "h1|0 in 1 -> v2".
"dirichl_bdAttrib" - string with attributes of edges with homogeneous Dirichlet boundary condition, e.g. "100; 102".

See also: refinehpFull

Author: Kersten Schmidt, 2009

◆ hpAdaptiveSpaceL2FromInput()

hpAdaptiveSpaceL2 * hp2D::hpAdaptiveSpaceL2FromInput	(	concepts::Mesh2 &	msh,
		const concepts::InOutParameters	input,
		bool	verbose = `false`
	)

Builds and refines a hp-adaptive 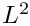-conforming space with use of input parameters.

As input parameter is needed:

"p" - an integer value for the polynomial degrees.

There may be used the input parameters:

"refinement"       - string with refinement rules, e.g. "h1|0 in 1 -> v2".
"dirichl_bdAttrib" - string with attributes of edges with homogeneous Dirichlet boundary condition, e.g. "100; 102"

"hpAdaptiveSpace_isTrunk" - boolean indicating the use of linear trunk space or not, by default, non trunk space is built.

See also: refinehpFull

Author: Kersten Schmidt, 2016

◆ operator<<()

template<typename DistClass , typename Function >

std::ostream & hp2D::operator<<	(	std::ostream &	os,
		const DistancePost< DistClass, Function > &	p
	)

inline

Definition at line 84 of file shortestDist.hh.

◆ refinehpFull()

void hp2D::refinehpFull	(	hp2D::hpFull &	prebuild,
		std::string	refinement
	)

Refines the space prebuilder prebuild where the refinement rules are given in the string refinement.

The string can consist of several refinement rules of the following form separated by commas, e.g. "p5, h3", which are applied one after the other.

There are the following refinement strategies.

"p"    - uniform polynomal degree enhancement (p-refinement)
"h"    - uniform refinement of the cells (h-refinement) or 
         h-refinement towards edges or vertices
"hp"   - geometrical hp-refinement towards edges or vertices

Each refinement strategy can be complemented with numbers.

"p5"   - polynomial degrees are enhanced by 5
"p2|1" - polynomial degree is first local direction of the quadrilateral
         is enhanced by 2, in the other direction by 1
"h2"   - twice uniform refinement of the cells
"h2|1" - twice uniform refinement of the cells in first local direction
         and a single refinement in the other direction
"hp2"  - twice geometrical hp-refinement towards edges or vertices

If a number is missing it means a single refinement or polynomial degree enhancement by 1.

Note, that the local directions of the quadrilateral are given by the order of the vertices. The first direction is from the 1st vertex to the 2nd or from the 4th to the 3th.

Each refinement rule can be restricted to a number of cells with a common attribute, e.g. "h in 1" means a uniform refinement in all cells with attribute 1.

For the h- and the hp-refinement rules vertices or edges can be given to which should be refined.

"h  -> v1"  - h-refinement  toward vertices with attribute 1
"h  -> e22" - h-refinement  toward edges with attribute 22
"hp -> v1"  - hp-refinement toward vertices with attribute 1
"hp -> e22" - hp-refinement toward edges with attribute 22

The cells touching these specified vertices and edges are refinement, and for hp-refinement the polynomial degrees in the other cells are increased by 1.

A combination of restriction towards cells and of refinement towards vertices or edges is possible, e.g. "h1|0 in 1 -> v2".

Author: Kersten Schmidt, 2009

◆ setQuadrature()

void hp2D::setQuadrature	(	enum concepts::intRule	rule,
		uint	noP
	)

Tensor integration setter routine in hp2D for hp2D::IntegrableQuads

Parameters

rule	Quadrature rule type, e.g. concepts::TRAPEZE, concepts::GAUSS_JACOBI
noP	constant number of quadrature points of given type

◆ setupAdvection()

template<class F >

void hp2D::setupAdvection	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< concepts::Point< F, 2 > >	frm,
		bool	transpose = `true`
	)

Function to setup a bilinear form related to the vector Advection, namely

$\sum_{i,j=1}^2 \int_K w_j u_i\frac{\partial v_i}{\partial x_j}\mathrm{d}x = \sum_{i=1}^2 \int_K \underline{w}\cdot\nabla v_i u_i \mathrm{d}x = \int_K \underline{w}^\top(\nabla\underline{v})^\top\underline{u}\mathrm{d}x$

if transpose is set to true or

$\sum_{i,j=1}^2 \int_K w_i u_j\frac{\partial v_i}{\partial x_j}\mathrm{d}x = \sum_{i=1}^2 \int_K w_i\underline{u}\cdot\nabla v_i \mathrm{d}x = \int_K \underline{w}^\top(\nabla\underline{v})\underline{u}\mathrm{d}x$

if transpose is set to false, both on vectorial spaces, where $\underline{u}$ and $\underline{v}$ are trial and test functions respectively, $\underline{w}$ is a given vectorial formula, and

$\nabla \underline{v} = \left(\begin{array}{cc} \frac{\partial u_1}{\partial x_1} & \frac{\partial u_1}{\partial x_2} \\ \frac{\partial u_2}{\partial x_1} & \frac{\partial u_2}{\partial x_2} . \end{array}\right)$

◆ setupDivDiv()

template<class F >

void hp2D::setupDivDiv	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >	frm = `concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >()`
	)

Function to setup a bilinear form

$\int_K f(x)\mathrm{div}\underline{u} \mathrm{div}\underline{v}\mathrm{d}x$

on vectorial spaces.

Examples: elasticity2D_tutorial.cc.

◆ setupGradLinearForm()

template<class F >

void hp2D::setupGradLinearForm	(	vectorial::LinearForm< F, typename concepts::Realtype< F >::type > &	lf,
		const concepts::ElementFormulaContainer< concepts::Point< F, 2 > >	frm1,
		const concepts::ElementFormulaContainer< concepts::Point< F, 2 > >	frm2
	)

Function to setup a linear form related to the vectorial linear form

$\int_K \underline{f}_1\cdot \mbox{\bf grad}{v_1} + \underline{f}_2\cdot \mbox{\bf grad}{v_2}\mathrm{d}x$

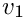
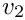
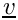
on vectorial spaces, where and are the first and second component of the test function $\underline{v}$ , respectively.

◆ setupIdDiv()

template<class F >

void hp2D::setupIdDiv	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< F >	frm = `concepts::ElementFormulaContainer< F >()`
	)

Function to setup a bilinear form related to the vector Identity, namely

$\int_K f(x) u \mathrm{div}\underline{v}\mathrm{d}x$

where the test space is a vectorial one.

◆ setupIdentity() [1/2]

template<class F >

void hp2D::setupIdentity	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< concepts::Mapping< F, 2 > >	frm,
		bool	transpose = `false`
	)

Function to setup a bilinear form related to the vector Identity, namely

$\int_K f(x) \underline{u}^\top A\underline{v}\mathrm{d}x$

on vectorial spaces. If transpose is true the transpose of the given matrix is taken.

◆ setupIdentity() [2/2]

template<class F >

void hp2D::setupIdentity	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< F >	frm = `concepts::ElementFormulaContainer< F >()`
	)

Function to setup a bilinear form related to the vector Identity, namely

$\int_K f(x) \underline{u}\cdot\underline{v}\mathrm{d}x$

on vectorial spaces.

◆ setupLaplace()

template<class F >

void hp2D::setupLaplace	(	vectorial::BilinearForm< F, typename concepts::Realtype< F >::type > &	bf,
		const concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >	frm = `concepts::ElementFormulaContainer< F, typename concepts::Realtype< F >::type >()`
	)

Function to setup a bilinear form related to the vector Laplace, namely

$\int_K f(x)\mathrm{grad}\underline{u}:\mathrm{grad}\underline{v}\mathrm{d}x$

on vectorial spaces.

◆ setupRiesz()

template<class F >

void hp2D::setupRiesz	(	vectorial::LinearForm< F, typename concepts::Realtype< F >::type > &	lf,
		const concepts::ElementFormulaContainer< concepts::Point< F, 2 > >	frm
	)

Function to setup a linear form related to the vector Riesz, namely

$\int_K \underline{f}\cdot\underline{v}\mathrm{d}x$

on vectorial spaces.

Class documentation of Concepts

Namespaces

Classes

Typedefs

Enumerations

Functions

Detailed Description

Typedef Documentation

◆ Adaptivity

◆ hpAdaptiveSpaceH1_DG

◆ hpAdaptiveSpaceL2_DG

Enumeration Type Documentation

◆ partDerivType

Function Documentation

◆ hpAdaptiveSpaceH1_DGFromInput()

◆ hpAdaptiveSpaceH1FromInput()

◆ hpAdaptiveSpaceHCurlFromInput()

◆ hpAdaptiveSpaceL2FromInput()

◆ operator<<()

◆ refinehpFull()

◆ setQuadrature()

◆ setupAdvection()

◆ setupDivDiv()

◆ setupGradLinearForm()

◆ setupIdDiv()

◆ setupIdentity() [1/2]

◆ setupIdentity() [2/2]

◆ setupLaplace()

◆ setupRiesz()