timestepping Namespace Reference

Classes
class	Alpha
class	Euler
class	LimitingEuler
class	LimitingTvdRK2
class	Newmark
class	Nystroem
class	RungeKutta2
class	RungeKutta4
class	Theta
class	TimeLinearForm
class	TimeStepping
class	TimeStepStrategy
class	TimeVector
class	TvdRK2

Detailed Description

Timestepping methods used to solve PDEs in time and space. The discretisation in space is done by the others parts of the library, the discretisation in time is done by this part of the library.

// Space
Line msh;
concepts::BoundaryConditions bc;      
linearFEM::Linear1d spc(msh, 4, bc.get());

// Space operators
Laplace stiff_bf;
concepts::SparseMatrix<Real> stiff(spc, stiff_bf);
Identity mass_bf(gauss_p);
concepts::SparseMatrix<Real> mass(spc, mass_bf);

// Zero initial conditions
concepts::Vector<Real> initial(spc)
concepts::Vector<Real> d_dt_initial(spc)

// External driver
Sin_tlf driver_tlf(1.0, 1.0 , 0.0, 0.0, 1);
timestepping::TimeVector driver(spc, driver_tlf);

// Strategy and Solver
timestepping::Newmark timeStepStrategy(mass, stiff, driver, initial,
                                       d_dt_initial, 0.01);
concepts::SuperLUFabric<> fabric;
timestepping::TimeStepping solver(timeStepStrategy, fabric);

// Write solutions to file in Gnuplot format
for(uint n = 0; n <= 5; ++n) {
  solver(sol, n*100/5);
  std::strstream filename;
  filename << "gnuplot/sol1d-" << n << ".gnuplot" << std::ends;
  graphics::DataGnuplot(spc, filename.str(), sol);
}

The follwing picture illustrates the wave equation solved on a rope.

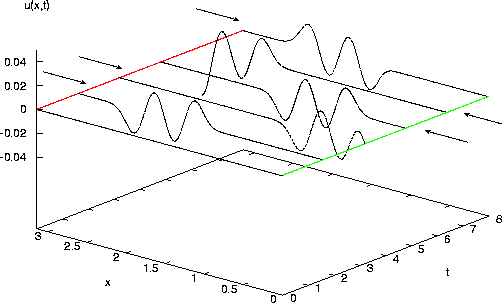
The red line indicates Neumann boundary conditions and the green line Dirichlet boundary conditions. The arrows point in the direction of the movent of the waves. One can clearly see the the waves are reflected on the boundaries and that they do change sign on the Dirichlet boundary and do not change sign on the Neumann boundary.

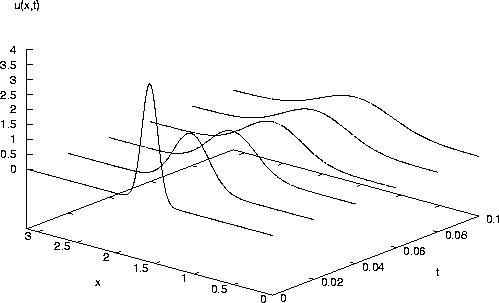
The next picture illustrates the heat equation solved on a wand: the intial peak flattens out as the heat dissipates. Boundary conditions are homogenous Dirichlet.

Author

Manuel Walser, 2002