Class documentation of Concepts
Enumerations | |
| enum | intRule { GAUSS_LOBATTO = 0 , GAUSS_JACOBI = 4 , TRAPEZE = 5 } |
| Types of integration rules to choose from. More... | |
| enum | Basis { Default = 0 , BND } |
| enum | Optimize { MIN , MAX } |
| enum | dimproj { dimX , dimY , dimZ , dimdiv } |
Detailed Description
Basic namespace for Concepts-2. Additional modules may be placed in a different namespace (or one which is nested into this one).
file geometry/cellConditions.hh
Boundary conditions
file geometry/connectorSequence.hh
Sets for Connectors.
- Todo:
- replace explicit occurrences of Pi by a namespace constant
@toolbox/resultsTable.hh
write table of results
Waveprop. Classes for physical sources and formulas for both Cartisian and Radial PML
Typedef Documentation
◆ Cmplx
| typedef std::complex<Real> concepts::Cmplx |
Type for a complex number. It also depends on the setting of Real.
- Examples
- arpackppTutorial.cc.
Definition at line 42 of file typedefs.hh.
◆ Cmplx1d
Definition at line 20 of file vectorsMatricesForward.hh.
◆ Cmplx2d
Definition at line 21 of file vectorsMatricesForward.hh.
◆ Cmplx3d
Definition at line 22 of file vectorsMatricesForward.hh.
◆ MapCmplx2d
Definition at line 627 of file vectorsMatrices.hh.
◆ MapCmplx3d
Definition at line 628 of file vectorsMatrices.hh.
◆ MapReal2d
Definition at line 625 of file vectorsMatrices.hh.
◆ MapReal3d
Definition at line 626 of file vectorsMatrices.hh.
◆ Real
Type normally used for a floating point number. The idea behind this: if you want to have single or quadruple precision instead of double precision, just change this typdef and recompile.
Definition at line 39 of file typedefs.hh.
◆ Real1d
Definition at line 17 of file vectorsMatricesForward.hh.
◆ Real2d
Definition at line 18 of file vectorsMatricesForward.hh.
◆ Real3d
Definition at line 19 of file vectorsMatricesForward.hh.
◆ Scan1
◆ Scan2
◆ Scan3
◆ ScanCntr0
◆ ScanCntr1
◆ ScanCntr2
◆ set_info
| typedef std::set<const std::type_info*> concepts::set_info |
Definition at line 23 of file matfileIO.hh.
◆ sint
Abbreviation for signed int.
Definition at line 45 of file typedefs.hh.
◆ uchar
Abbreviation for unsigned char.
Definition at line 48 of file typedefs.hh.
◆ Unit1d
Definition at line 27 of file vectorsMatricesForward.hh.
◆ Unit2d
Definition at line 28 of file vectorsMatricesForward.hh.
◆ Unit3d
Definition at line 29 of file vectorsMatricesForward.hh.
◆ ushort
Abbreviation for unsigned short.
Definition at line 51 of file typedefs.hh.
Enumeration Type Documentation
◆ Basis
Enum representing the basis evaluation type of a Linearform ALL - standard linearform evaluation on all basis functions of a element BND - linearform evaluation just on basisfunctions on the boundary, in 1D : nodal in 2D : nodal and edge basis in 3D : nodal, edge, face this applicates for tensored basis functions on hp2D::Quad only at the moment.
Note that in the BND case for tensored quad the Elementmatrix have different size, i.e. em.size = 2 in 1D, em.size = 2*(elm.px + elm.py) in 2D, ... The order stays first x then y.
Further possible types : INNER, etc..
Definition at line 55 of file linearForm.hh.
◆ dimproj
| enum concepts::dimproj |
Definition at line 32 of file DtNmap2D_visc.hh.
◆ intRule
Types of integration rules to choose from.
Definition at line 13 of file defines.hh.
◆ Optimize
| enum concepts::Optimize |
Definition at line 26 of file extrema.hh.
Function Documentation
◆ addExactDtN_Circle2D() [1/2]
◆ addExactDtN_Circle2D() [2/2]
| void concepts::addExactDtN_Circle2D | ( | Matrix< Real > & | dest, |
| const SpaceOnCells< Real > & | spc, | ||
| const Sequence< Real > | DtNCoeff | ||
| ) |
Add DtN contribution for a circular boundary
- Parameters
-
dest Matrix for the problem formulation spc Space defined on the DtN boundary DtNCoeff coefficients of the DtN map
- Examples
- exactDtN.cc.
◆ addExactDtN_X_2Dcos_wp()
| void concepts::addExactDtN_X_2Dcos_wp | ( | Matrix< Cmplx > & | dest, |
| const SpaceOnCells< Real > & | spc, | ||
| const Sequence< F > | DtNCoeff, | ||
| Vector< Cmplx > & | rhs, | ||
| const G & | frm, | ||
| const Sequence< F > | DtNCoeffRhs, | ||
| const Real | L = 1.0 |
||
| ) |
Definition at line 214 of file DtNmap2D_visc.hh.
◆ addExactDtN_X_2Dcossin_wp()
| void concepts::addExactDtN_X_2Dcossin_wp | ( | Matrix< Cmplx > & | dest, |
| const SpaceOnCells< Real > & | spc, | ||
| const Sequence< F > | DtNCoeff, | ||
| Vector< Cmplx > & | rhs, | ||
| const G & | frm, | ||
| const Sequence< F > | DtNCoeffRhs, | ||
| const Real | L = 1.0 |
||
| ) |
Definition at line 251 of file DtNmap2D_visc.hh.
◆ addExactDtN_X_2Dsin_wp()
| void concepts::addExactDtN_X_2Dsin_wp | ( | Matrix< Cmplx > & | dest, |
| const SpaceOnCells< Real > & | spc, | ||
| const Sequence< F > | DtNCoeff, | ||
| Vector< Cmplx > & | rhs, | ||
| const G & | frm, | ||
| const Sequence< F > | DtNCoeffRhs, | ||
| const Real | L = 1.0 |
||
| ) |
Definition at line 233 of file DtNmap2D_visc.hh.
◆ addExactDtN_X_2Dsincos_wp()
| void concepts::addExactDtN_X_2Dsincos_wp | ( | Matrix< Cmplx > & | dest, |
| const SpaceOnCells< Real > & | spc, | ||
| const Sequence< F > | DtNCoeff, | ||
| Vector< Cmplx > & | rhs, | ||
| const G & | frm, | ||
| const Sequence< F > | DtNCoeffRhs, | ||
| const Real | L = 1.0 |
||
| ) |
Definition at line 274 of file DtNmap2D_visc.hh.
◆ adjugate() [1/2]
Definition at line 33 of file operations.hh.
◆ adjugate() [2/2]
Definition at line 30 of file operations.hh.
◆ allConnectors() [1/2]
Return all connectors of a particular type of another connector, e.g. all edges of a cell
Sequence<Connector1*> edges = allConnectors(cntr, &Connector2::edge);
Definition at line 126 of file connectorSequence.hh.
◆ allConnectors() [2/2]
Return all connectors of a particular type of another connector, e.g. all edges of a cell
Set<Connector1*> edges; allConnectors(cntr, &Connector2::edge, edges);
Definition at line 177 of file connectorSet.hh.
◆ apply()
◆ besselJn()
Evaluates the Bessel function 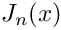
Evaluates the Bessel function 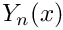
◆ buildEdgeMesh()
| void concepts::buildEdgeMesh | ( | Scan2 * | sc, |
| const concepts::Set< uint > | attrib, | ||
| MutableMeshBase & | emsh | ||
| ) |
Construct a mesh of edges of a 2D mesh w.r.t. to particular attributes.
- Parameters
-
sc Scanner over the cells of the 2D mesh. attrib Set of edge attributes. emsh Edge mesh to which the elements on the edge are added.
Currently work only for Quad2d as they are only provide a method to generate a cell for an edge.
Typical call
concepts::MutableMesh1 edgeMsh; concepts::Set<uint> eAttrib; eAttrib.insert(2); concepts::buildEdgeMesh(msh.scan(), eAttrib, edgeMsh);
The mesh on edges takes over the parent-child relationship from the quadrilateral mesh. But, after construction the meshes are independent meaning that refinement in one mesh is not automatically followed by the other.
The topological objects (connectors) are hold outside, most probably by the 2D mesh which must consequently not be deleted.
◆ chebychevPoints()
|
inline |
Zeros of Chebychev polynomials in [-1,1].
Number of points is given by the size of the array.
Definition at line 130 of file arrayOp.hh.
◆ componentArray()
Returns the component array of an array of vectors
- Parameters
-
i component
Definition at line 145 of file arrayOp.hh.
◆ computeKarniadakisValues()
|
inline |
Evaluate (transformed) Karniadakis Shapefunctions up to a order np on requested abcissa points in [0,1]. Per standard Karniadakis Shapefunctions are defined on [-1,1]. Here they are given analytical as polynomial transformed on [0,1].
This applicates as following: Let us say we want to evaluate the original shapefunction at the point -1 + eps. For too small eps, we observe cancellation effect due to mashine precision. As a consequence since almost all karniadakis polynomials are zero at -1, they will be evaluated as zero due to the cancelation effect. To avoid this, integration points are computed numerical stable on [0,1], with small values delta around 0. Now the analytical given shapefunctions on [0,1] can be evaluated close to zero, without mentionable cancellation effect.
Note that the second basis function, namely 1-x, as well like almost all derivatives are evaluated with cancellation effect near to zero.
Those evaluations are done by recursion formulas, directly derived from recursion formulas of the jacobian polynomials on [-1,1].
- Parameters
-
np evaluate shapefuntions up to order np, i.e np+1 shapefunctions, that is for np=2 (1-x) x x(1-x) absc abcissa points in [0,1], must be preallocated npx number of abcissa points type 0 for Karniadakis<1, 0> normal 1 for Karniadakis<1, 1> derivative
Definition at line 46 of file karniadakisOp.hh.
◆ convertCCS_rowSorting()
| void concepts::convertCCS_rowSorting | ( | F & | m, |
| typename F::type * | a, | ||
| int * | asub, | ||
| int * | xa | ||
| ) |
Method converts a matrix of type F to Sparse Column Storage (CCS) format. The matrix type needs an iterator over the entrances, which moves at least row by row. Inside the row the entrances are sorted by column before writing to the output arrays.
- Parameters
-
m matrix a array of values asub array of row indices xa arrays of column pointers
◆ convertCRS_rowSorting()
| void concepts::convertCRS_rowSorting | ( | F & | m, |
| typename F::value_type * | a, | ||
| int * | asub, | ||
| int * | xa | ||
| ) |
Method converts a matrix of type F to Sparse Row Storage (CRS) format. The matrix type needs an iterator over the entrances, which moves at least row by row. Inside the row the entrances are sorted by column before writing to the output arrays.
- Parameters
-
m matrix a array of values asub array of column indices xa arrays of row pointers
◆ convertIJK_unSorted()
◆ createBelosSolverMgr()
| Teuchos::RCP< Belos::SolverManager< T, Tpetra::MultiVector< T, int >, Tpetra::Operator< T > > > concepts::createBelosSolverMgr | ( | std::string | solverType, |
| const Teuchos::RCP< Teuchos::ParameterList > & | solverParam, | ||
| Teuchos::RCP< Belos::LinearProblem< T, Tpetra::MultiVector< T, int >, Tpetra::Operator< T > > > | linearProblem | ||
| ) |
Sets the solver type to one of the followings
"GMRES""BLOCKCG""PSEUDOCG"
Definition at line 36 of file belosSolver_decl.hh.
◆ createIfpackPrec()
| Teuchos::RCP< Ifpack2::Preconditioner< T > > concepts::createIfpackPrec | ( | std::string | precType, |
| Teuchos::RCP< Teuchos::ParameterList > | precParam, | ||
| const Teuchos::RCP< const Tpetra::CrsMatrix< T, int > > | A | ||
| ) |
precType can assume the following parameters
"DIAGONAL""RELAXATION""CHEBYSHEV""ILUT""RILUK"
Definition at line 87 of file belosSolver_decl.hh.
◆ demangle()
| std::string concepts::demangle | ( | const char * | name | ) |
Returns the class name of a typeid name return statement. This is a inbuild solution for the |c++filt -t option, when calling the program*
- Parameters
-
name Name of the typeid
- Remarks
- If the compiler is not gcc, this function returns exactly std::string(name)
◆ determinant()
Definition at line 27 of file operations.hh.
◆ ensureEnding()
| std::string concepts::ensureEnding | ( | const std::string & | filename, |
| const std::string | ending | ||
| ) |
Returns a string with particular ending. Append it, if needed.
◆ evaluatepermutation()
Evaluation of a 3d permutation
We consider the following evaluation conventions
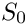
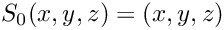
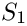
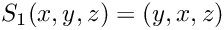
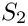
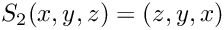
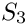
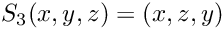
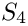
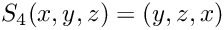
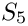
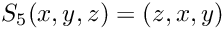
- Parameters
-
p point to evaluate index index of the permutation
◆ exception_set_fields()
| exc concepts::exception_set_fields | ( | exc | e, |
| const std::string & | file, | ||
| const unsigned int | line, | ||
| const std::string & | function, | ||
| const std::string & | excName | ||
| ) |
Sets fields on exception and throws it. This routine does the main work for the conceptsException macro. This routine should not be called directly, it is used by the conceptsException macro.
- Returns
- An exception which can then be thrown
- Parameters
-
e Exception to be thrown file Filename where the exception was thrown from line Line where the exception was thrown from function Name of the function that threw the exception excName The name of the exception
- See also
- conceptsException
- ExceptionBase
Definition at line 316 of file exceptions.hh.
◆ exception_throw_assert()
| void concepts::exception_throw_assert | ( | const std::string & | file, |
| int | line, | ||
| const std::string & | function, | ||
| const std::string & | exc_name, | ||
| const std::string & | cond, | ||
| exc | e | ||
| ) |
Sets the fields of an assertion and throws it. This routine does the main work for the exception generation mechanism used in the conceptsAssert macro. This routine should not be called directly, it is used by the conceptsAssert macro.
- See also
- conceptsAssert
- Assertion
Definition at line 364 of file exceptions.hh.
◆ g_fast()
◆ g_slow()
◆ GaussJacobiAbscWght()
Computes and returns the integration weights and abscissas for the Gauss Jacobi integration. The abscissas no not include the endpoints -1 and 1.
Integration with the quadrature rule
![\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]](form_619.png)
is exact for polynomials 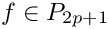
The abscissas 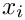
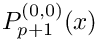
![\[w_i = \frac{2}{1-x_i^2} \left( \frac{d}{dx} \left. P^{(0,0)}_{p+1}(x) \right|_{x=x_i} \right)^{-2}.\]](form_637.png)
- Precondition
- The space for the arrays x and w is allocated, size: p+1.
◆ GaussLobattoAbscWght()
Computes and returns the integration weights and abscissas for the Gauss (Jacobi) Lobatto integration. The Jacobi version can be chosen with a parameter. The abscissas include both endpoints, ie. 1 and -1.
Integration with the quadrature rule
![\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]](form_619.png)
is exact for polynomials 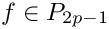
![\[ \int_{-1}^1 f(x) (1-x)^j \, dx \approx \sum_{i=0}^p w_i f(x_i) \]](form_649.png)
exactly for 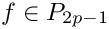
The abscissas 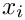
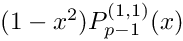
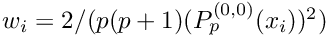
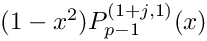
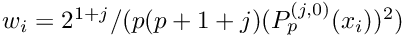
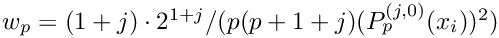
- Parameters
-
x Output: the integration abscissas w Output: the integration weights p Order of the integration, p+1 points are computed j The Jacobi version of the integration rule is used if this is non-zero.
- Precondition
- The space for the arrays x and w is allocated, size: p+1.
◆ GaussRadauAbscWght()
Computes and returns the integration weights and abscissas for the Gauss Radau Jacobi integration. The Jacobi version can be chosen with a parameter. The abscissas include only one endpoint: -1.
Integration with the quadrature rule
![\[ \int_{-1}^1 f(x) \, dx \approx \sum_{i=0}^p w_i f(x_i) \]](form_619.png)
is exact for polynomials 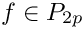
![\[ \int_{-1}^1 f(x) (1-x)^j \, dx \approx \sum_{i=0}^p w_i f(x_i) \]](form_649.png)
exactly for 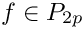
The abscissas 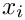
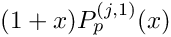
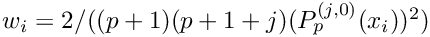
- Parameters
-
x Output: the integration abscissas w Output: the integration weights p Order of the integration, p+1 points are computed j The Jacobi version of the integration rule is used if this is non-zero.
- Precondition
- The space for the arrays x and w is allocated, size: p+1.
◆ getChild()
| void concepts::getChild | ( | const typename JacobianCell< dimC >::cell & | cCell, |
| const Point< Real, dimC > & | eta, | ||
| const std::array< Real, std::size_t(dimC)> | x0, | ||
| const std::array< Real, std::size_t(dimC)> | xN, | ||
| const typename JacobianCell< dimC >::cell *& | cld | ||
| ) |
Searches through the dichotomic tree cell hierachy to find the unique child cell that is defined via the local point eta in [0,1]^dimC
- Precondition
- the coarse Cells children if existing are preallocated, and introduce pointers
- eta is in [0,1]^dimC for speed up
◆ getFilenamePrefix()
| std::string concepts::getFilenamePrefix | ( | const std::string | str | ) |
Returns the prefix of a given full filename, e.g.. "example" for "~/example.dat".
◆ getHelmholtzDtNCoeff_Circle2D()
| Sequence< Cmplx > concepts::getHelmholtzDtNCoeff_Circle2D | ( | const Real | omega, |
| const Real | R, | ||
| uint | N = 0 |
||
| ) |
Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a circular boundary of radius R which is truncated at order N.
- Parameters
-
L width of the boundary N truncation order
- Examples
- exactDtN.cc.
◆ getHelmholtzDtNCoeff_Feng_Circle2D()
| Sequence< Cmplx > concepts::getHelmholtzDtNCoeff_Feng_Circle2D | ( | const Real | R, |
| const Real | k, | ||
| unsigned int | N | ||
| ) |
Returns the coefficients for a local DtN map of Feng for the Helmholtz equation with wave number k for a circular boundary of radius R of order N for orders 0 to 5.
- Parameters
-
R radius of the circular domain k wave number N order of Feng's condition (0,1,2,3,4 or 5)
◆ getHelmholtzDtNCoeff_Straight2D()
| Sequence< Cmplx > concepts::getHelmholtzDtNCoeff_Straight2D | ( | const Real | omega, |
| const Real | L, | ||
| uint | N = 0 |
||
| ) |
Returns the coefficients for a non-local DtN map for the Helmholtz operator with frequency omega for a straight boundary of length L which is truncated at order N.
In the strip ![$[0,L]\times[0,\infty)$](form_680.png)
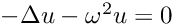
![\[u(x,y) = a_0 \exp(k_0 y) + \sum_{n=1}^N \left( a_n \cos(2\pi n\frac{x}{L}) +
b_n \sin(2\pi n\frac{x}{L})\right)
\mathrm{e}^{k_n y}
\]](form_689.png)
with
![\[
a_0 = \frac{1}{L}\int_{0}^L u(x',0) \mathrm{d}x', \\
a_n = \frac{2}{L}\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x', \\
b_n = \frac{2}{L}\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x', \\
k_n = \imath \sqrt{\omega^2 - \Big( \frac{n \pi}{L}\Big)^2}, \quad \omega > \frac{n \pi}{L}, \\
k_n = - \sqrt{\Big( \frac{n \pi}{L}\Big)^2 - \omega^2}, \quad \text{otherwise}.
\]](form_690.png)
The normal derivative at 
![\[
\partial_y u(x,0) = a_0 k_0 +
\sum_{n=1}^N k_n \left( a_n \cos(2\pi n\frac{x}{L}) +
b_n \sin(2\pi n\frac{x}{L})\right)
\]](form_691.png)
and so
![\[
\int_0^L \partial_y u(x,0) v(x,0) \mathrm{d}x
= \frac{k_0}{L} \int_0^L u(x',0) \mathrm{d}x' \int_0^L v(x,0) \mathrm{d}x
+ \sum_{n=1}^N \frac{k_n}{L}\left(
2\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x'
\int_{0}^L v(x ,0) \cos(2\pi n\frac{x }{L})\mathrm{d}x +
2\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x'
\int_{0}^L v(x ,0) \sin(2\pi n\frac{x }{L})\mathrm{d}x
\right)
\]](form_692.png)
The factor 2 is used to have the same coefficients for an derivation with 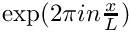
- Parameters
-
omega wave pulse L width of the boundary N truncation order
◆ getLaplaceDtNCoeff_Circle2D()
Returns the coefficients for a non-local DtN map for the Laplace operator for a circular boundary of radius R which is truncated at order N.
- Parameters
-
omega wave pulse L width of the boundary N truncation order
◆ getLaplaceDtNCoeff_Straight2D()
Returns the coefficients for a non-local DtN map for the Laplace operator for a straight boundary of length L which is truncated at order N.
In the strip ![$[0,L]\times[0,\infty)$](form_680.png)
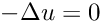
![\[u(x,y) = a_0 + \sum_{n=1}^N \left( a_n \cos(2\pi n\frac{x}{L}) +
b_n \sin(2\pi n\frac{x}{L})\right)
\mathrm{e}^{-2\pi n\frac{y}{L}}
\]](form_682.png)
with
![\[
a_0 = \frac{1}{L}\int_{0}^L u(x',0) \mathrm{d}x'
a_n = \frac{2}{L}\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x',\\
b_n = \frac{2}{L}\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x'.
\]](form_683.png)
The normal derivative at 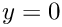
![\[
\partial_y u(x,0) =
\sum_{n=1}^N -\frac{2\pi n}{L}\left( a_n \cos(2\pi n\frac{x}{L}) +
b_n \sin(2\pi n\frac{x}{L})\right)
\]](form_685.png)
and so
![\[
\int_0^L -\partial_y u(x,0) v(x,0) \mathrm{d}x
= \sum_{n=1}^N \frac{2\pi n}{L^2}\left(
2\int_{0}^L u(x',0) \cos(2\pi n\frac{x'}{L})\mathrm{d}x'
\int_{0}^L v(x ,0) \cos(2\pi n\frac{x }{L})\mathrm{d}x +
2\int_{0}^L u(x',0) \sin(2\pi n\frac{x'}{L})\mathrm{d}x'
\int_{0}^L v(x ,0) \sin(2\pi n\frac{x }{L})\mathrm{d}x
\right)
\]](form_686.png)
The factor 2 is used to have the same coefficients for an derivation with 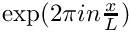
Note, that as for the Laplace problem with pure Neumann boundary conditions the constant may not be defined (DtN coefficient for 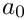
- Parameters
-
L width of the boundary N truncation order
◆ getNSDtNCoeff_Straight2D_partDn()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partDn | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 0 |
||
| ) |
Definition at line 123 of file DtNmap2Dvisc.hh.
◆ getNSDtNCoeff_Straight2D_partDt()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partDt | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 1 |
||
| ) |
Definition at line 146 of file DtNmap2Dvisc.hh.
◆ getNSDtNCoeff_Straight2D_partDttilde()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partDttilde | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 1 |
||
| ) |
Definition at line 169 of file DtNmap2Dvisc.hh.
◆ getNSDtNCoeff_Straight2D_partRn()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partRn | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 1 |
||
| ) |
Definition at line 191 of file DtNmap2Dvisc.hh.
◆ getNSDtNCoeff_Straight2D_partRntilde()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partRntilde | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 1 |
||
| ) |
Definition at line 214 of file DtNmap2Dvisc.hh.
◆ getNSDtNCoeff_Straight2D_partRt()
| Sequence< Cmplx > concepts::getNSDtNCoeff_Straight2D_partRt | ( | const Real | L, |
| const Real | omega, | ||
| const Real | c, | ||
| const Real | rho0, | ||
| const Real | nu, | ||
| uint | N = 0 |
||
| ) |
Definition at line 236 of file DtNmap2Dvisc.hh.
◆ getNumberofRows() [1/2]
◆ getNumberofRows() [2/2]
| uint concepts::getNumberofRows | ( | HashedSparseMatrix< F > & | m | ) |
Definition at line 275 of file hashedSMatrix.hh.
◆ hankel_1_deriv_n()
Evaluates the derivative 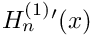

◆ hankel_1_n()
◆ hankel_2_deriv_n()
Evaluates the derivative 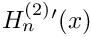
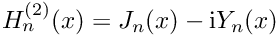
◆ hankel_2_n()
◆ import2dMeshGeneralFromInput()
| Import2dMeshGeneral * concepts::import2dMeshGeneralFromInput | ( | const InOutParameters | input, |
| bool | verbose = false |
||
| ) |
Loads a mesh from a paramater list.
The parameter list needs the strings: "inputfilename" - prefix for all file names.
The parameter list may include the strings: "inputpath" - name of the path where the files are inside. If not given, the current working directory (".") is taken.
It will be excepted five files, namely the coordinate, the element, the attribute, the edge radia and the edge correlation file of the following names. Let the prefix be "example". Then, the files are "example_Coord.dat", "example_Elms.dat", "example_Attr.dat", "example_EdgRadia.dat", "example_EdgCorr.dat".
The files have to exist, but may be empty.
- Examples
- cig_load_input_data.cc, and elasticity2D_tutorial.cc.
◆ integrate() [1/6]
Returns the area of the cell belonging to the element elm.
Definition at line 43 of file integral.hh.
◆ integrate() [2/6]
| F concepts::integrate | ( | const ElementWithCell< G > & | elm, |
| const ElementFormula< F, G > & | frm, | ||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the integral of the element formula frm over the cell belonging to the element elm.
Definition at line 64 of file integral.hh.
◆ integrate() [3/6]
| F concepts::integrate | ( | const ElementWithCell< G > & | elm1, |
| const ElementWithCell< G > & | elm2, | ||
| const ElementFormula< F, G > & | frm1, | ||
| const ElementFormula< F, G > & | frm2, | ||
| const Real | t = 0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the integral over the element elm1 respective elm2 of the product of the ElementFormulas frm1 and frm2. The two elements must use the same topological cells.
Definition at line 154 of file integral.hh.
◆ integrate() [4/6]
| F concepts::integrate | ( | const Sequence< ElementWithCell< G > * > & | elm_seq, |
| const ElementFormula< F, G > & | frm, | ||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the integral over elements in sequence elm_seq of the formula or element formula frm at time t. The integration form is form.
Cells are valid, if they are derivated from IntegrationCell.
- See also
- IntegrationCell
Definition at line 131 of file integral.hh.
◆ integrate() [5/6]
| F concepts::integrate | ( | const SpaceOnCells< G > & | spc, |
| const ElementFormula< F, G > & | frm, | ||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the integral over space spc of the formula or element formula frm at time t. The integration form is form.
Spaces are valid, if their elements are derivated from IntegrationCell.
- See also
- IntegrationCell
Definition at line 96 of file integral.hh.
◆ integrate() [6/6]
| F concepts::integrate | ( | const SpaceOnCells< G > & | spc1, |
| const SpaceOnCells< G > & | spc2, | ||
| const ElementFormula< F, G > & | frm1, | ||
| const ElementFormula< F, G > & | frm2, | ||
| const Real | t = 0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the integral over spc1 respective spc2 of the product of the ElementFormulas frm1 and frm2, where frm1 is given on spc1 and frm2 is given on spc2. The two spaces must use the same topological cells. This method can be used for integrals over interfaces.
Definition at line 182 of file integral.hh.
◆ inverse() [1/4]
| F concepts::inverse | ( | const F & | f | ) |
Definition at line 18 of file operations.hh.
◆ inverse() [2/4]
Definition at line 24 of file operations.hh.
◆ inverse() [3/4]
| F & concepts::inverse | ( | F & | f | ) |
Definition at line 15 of file operations.hh.
◆ inverse() [4/4]
Definition at line 21 of file operations.hh.
◆ isParallelRunning()
| bool concepts::isParallelRunning | ( | ) |
Tests if the instruction MPI::Init() was called
- Remarks
- This method can also be called in sequential compiling, therefore will always return false
◆ jacobianDeterminant() [1/2]
| Array< Real > concepts::jacobianDeterminant | ( | const Hexahedron3d & | Hexa, |
| const Array< QuadratureRule1d * > & | ArrayQuad1D | ||
| ) |
Computes a multi-dimensional Jacobian determinant tensor
- Parameters
-
Hexa mapped hexahedron to consider ArrayQuad1D pointers to 1D quadratures
◆ jacobianDeterminant() [2/2]
| Real concepts::jacobianDeterminant | ( | const Hexahedron3d & | Hexa, |
| const Real3d & | xi | ||
| ) |
Computes the Jacobian determinant 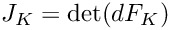
- Parameters
-
Hexa mapped hexahedron to consider xi reference element in the cube 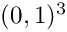
◆ jacobianTensor() [1/2]
| Array< Mapping< Real, 3, 3 > > concepts::jacobianTensor | ( | const Hexahedron3d & | Hexa, |
| const Array< QuadratureRule1d * > & | ArrayQuad1D | ||
| ) |
Computes a multi-dimensional Jacobian tensor
- Parameters
-
Hexa mapped hexahedron to consider ArrayQuad1D pointers to 1D quadratures
◆ jacobianTensor() [2/2]
| Mapping< Real, 3, 3 > concepts::jacobianTensor | ( | const Hexahedron3d & | Hexa, |
| const Real3d & | xi | ||
| ) |
Compute the Jacobian tensor 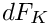
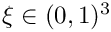
- Parameters
-
Hexa mapped hexahedron to consider xi reference element in the cube 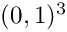
◆ JacobiDerivatives()
| void concepts::JacobiDerivatives | ( | const double | alf, |
| const double | bet, | ||
| const int | maxn, | ||
| const double * | x, | ||
| const int | m, | ||
| const double * | p, | ||
| double * | q | ||
| ) |
Computes the values of the derivatives of the Jacobi polynomials.
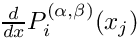

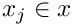
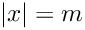
- Parameters
-
alf 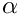
bet 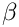
maxn Highest polynomial degree to be computed x Array of size mwith the points in which the polynomials should be evaluated.![$x_j \in [-1,1]$](form_646.png)
m Size of array xp Array of the size m*(maxn+1) filled with the Jacobi polynomials.q Array of the size m*(maxn+1) (must be allocated), will be filled with the values of the derivatives of the poynomials in the points withirunning fastest.
- Precondition
- The space for the array
qis allocated, size:m*(maxn+1)
◆ JacobiPol()
| void concepts::JacobiPol | ( | const double | alf, |
| const double | bet, | ||
| const int | maxn, | ||
| const double * | x, | ||
| const int | m, | ||
| double * | p | ||
| ) |
Computes the values of the Jacobi polynomials.


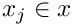
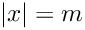
- Parameters
-
alf 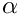
bet 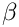
maxn Highest polynomial degree to be computed x Array of size mwith the points in which the polynomials should be evaluated.![$x_j \in [-1,1]$](form_646.png)
m Size of array xp Array of the size m*(maxn+1) (must be allocated), will be filled with the values of the poynomials in the points with i running fastest.
- Precondition
- The space for the array
pis allocated, size: m*(maxn+1)
◆ JacobiZeros()
Computes the zeros of the Jacobi polynomials 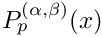
- Parameters
-
x Output: the zeros of the Jacobi polynomials in the elements 1, ..., p. The element 0 of the array is untouched. p Degree of the Jacobi polynomial alf 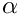
bet 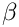
- Precondition
- The space for the arrays x is allocated, size: p+1
◆ L2product() [1/3]
| Real concepts::L2product | ( | const ElementWithCell< G > & | elm, |
| const ElementFormula< F, G > & | u, | ||
| const ElementFormula< Real > * | c = 0, |
||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the L2 product or with c weighted L2 product of an element formula u over the cell belonging to the element elm.
![\[\int\limits_{K}c u^\top\cdot\overline{u}\,dx\]](form_750.png)
- Examples
- parallelizationTutorial.cc.
Definition at line 214 of file integral.hh.
◆ L2product() [2/3]
| Real concepts::L2product | ( | const Sequence< ElementWithCell< G > * > & | elm_seq, |
| const ElementFormula< F, G > & | u, | ||
| const ElementFormula< Real > * | c = 0, |
||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the L2 product or with c weighted L2 product of an element formula u over the cells belonging to the elements in the sequence elm_seq.
![\[\int\limits_{K}c u^\top\cdot\overline{u}\,dx\]](form_750.png)
Definition at line 296 of file integral.hh.
◆ L2product() [3/3]
| Real concepts::L2product | ( | SpaceOnCells< F > & | spc, |
| const G & | u, | ||
| const ElementFormula< Real > * | c = 0, |
||
| const Real | t = 0.0, |
||
| IntegrationCell::intFormType | form = IntegrationCell::ZERO |
||
| ) |
Returns the L2 product or with c weighted L2 product over space spc of the formula or element formula u at time t. The integration form is form.
![\[\int\limits_{\Omega}c u^\top\cdot\overline{u}\,dx\]](form_751.png)
Spaces are valid, if their elements are derivated from IntegrationCell.
- See also
- IntegrationCell
Definition at line 267 of file integral.hh.
◆ lambda_j_fast()
◆ lambda_j_slow()
◆ lambda_limit()
Definition at line 82 of file DtNmap2D_visc.hh.
◆ makeAdaptiveQuadrature()
| std::shared_ptr< const FunctionT > concepts::makeAdaptiveQuadrature | ( | const uint | nQuadraturePoints, |
| const intRule | quadratureType | ||
| ) |
factory function encapsulating the memory manager
FIXME: code factorization
Definition at line 191 of file flyweight.hh.
◆ makeArray() [1/4]
◆ makeArray() [2/4]
| void concepts::makeArray | ( | const F & | cell, |
| const Array< Real > & | pX, | ||
| const Array< Real > & | pY, | ||
| const Array< Real > & | pZ, | ||
| G(F::*)(Real, Real, Real) const | fun, | ||
| Array< G > & | array, | ||
| bool | istensor = true |
||
| ) |
Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY. The fast loop is over pY for tensor basis case.
Also for non tensor case, there is one loop over all integration points (pX(i), pY(i)), i = 0,..., points.
◆ makeArray() [3/4]
| void concepts::makeArray | ( | const F & | cell, |
| const Array< Real > & | pX, | ||
| const Array< Real > & | pY, | ||
| G(F::*)(Real, Real) const | fun, | ||
| Array< G > & | array, | ||
| bool | istensor = true |
||
| ) |
Creates an array array by applying an function fun of a cell cell for each combination of the values pX and pY. The fast loop is over pY for tensor basis case.
Also for non tensor case, there is one loop over all integration points (pX(i), pY(i)), i = 0,..., points.
◆ makeArray() [4/4]
Creates an array from a comma separated list of values.
For example,
makeArray<int>({2, 3, 6, 7})creates an array of 4 elements containing [2, 3, 6, 7].
Definition at line 114 of file arrayOp.hh.
◆ makecRCP_weak()
Definition at line 129 of file sharedPointer_boost.hh.
◆ makeEquidistantSequence()
| Sequence< F > concepts::makeEquidistantSequence | ( | uint | n, |
| const F & | first, | ||
| const F & | diff | ||
| ) |
Definition at line 407 of file sequence.hh.
◆ makeQuadrature()
| std::shared_ptr< const FunctionT > concepts::makeQuadrature | ( | const uint | nQuadraturePoints, |
| const intRule | quadratureType | ||
| ) |
factory function encapsulating the memory manager
Bring here a polymorphic constructor
Definition at line 154 of file flyweight.hh.
◆ makeRangeSequence()
Returns the sequence start, start+dist,... such that last entry is smaller than afterlast
◆ makeRCP()
Function to create a RCP which deletes the object when no RCP points on it anymore.
The function has to be used, if the object is created with new.
For example:
RCP<int>::Type iP = makeRCP(new int(2)); iP.reset(); // deletes the integer 2
Second example:
RCP<int>::Type iP = makeRCP(new int(3)), jP = iP; jP.reset(); // does not delete the integer 3, as jP points still on it iP.reset(); // deletes the integer 3, no RCP points on it
Definition at line 102 of file sharedPointer_boost.hh.
◆ makeRCP_weak()
Function to create a RCP without deleting the object in the destructor
The function has to be used, if the object remains externally, e.g., in the heap.
For example:
int i = 1; RCP<int>::Type iP = makeRCP_weak(&i); iP.reset(); // will not delete the integer 1
Definition at line 122 of file sharedPointer_boost.hh.
◆ makeSequence() [1/2]
Creates an sequence of length
from a comma separated list of values.
e.g.
makeSequence(2, 3, 6, 7)
creates an sequence [2, 3, 6, 7]
Definition at line 395 of file sequence.hh.
◆ makeSequence() [2/2]
Creates an sequence of length
from a comma separated list of values.
e.g.
makeSequence(4, 2, 3, 6, 7)
creates an sequence [2, 3, 6, 7]
Definition at line 375 of file sequence.hh.
◆ makeSet() [1/2]
| Set< F > concepts::makeSet | ( | std::initializer_list< F > | list | ) |
◆ makeSet() [2/2]
| Set< F > concepts::makeSet | ( | uint | n, |
| const F & | first, | ||
| ... | |||
| ) |
Creates an array of length
from a comma separated list of values.
e.g.
makeSet(4, 3, 2, 6, 7)
creates an set [2, 3, 6, 7]
- Examples
- BGT_0.cc, elasticity2D_tutorial.cc, exactDtN.cc, hpFEM2d.cc, meshes.cc, and parallelizationTutorial.cc.
◆ makeShapeFunction()
| std::shared_ptr< const FunctionT > concepts::makeShapeFunction | ( | const concepts::QuadratureRule1d & | quadratureRule, |
| const uint | polynomialDegree | ||
| ) |
factory function encapsulating the memory manager
Definition at line 122 of file flyweight.hh.
◆ match()
| int concepts::match | ( | const Connector1 & | edg0, |
| const Connector1 & | edg1, | ||
| int | idx[] | ||
| ) |
Checks, if two edges has a common vertex. In that case the value 1 is returned, and the idx[0]-th vertex of edg0 coincide with the idx[1]-th vertex of edg1.
◆ matrixMultiplyRowSorting()
Multiplies two matrices, which deliver at least a row sorted iterator, and adds (!) the result to a third matrix.
The matrices factL and factR needs the methods nofRows(), nofCols(), begin(row) or begin() respectivly.
Definition at line 28 of file matrixMult.hh.
◆ memorycpy()
Copies n entries from src to dest (faster than std::memcpy)
Definition at line 31 of file vectorsMatrices.hh.
◆ newField()
◆ operator!=() [1/2]
|
inline |
Definition at line 150 of file matrixIterator.hh.
◆ operator!=() [2/2]
|
inline |
Definition at line 158 of file matrixIterator.hh.
◆ operator*() [1/9]
| BilinearFormContainer< Real > concepts::operator* | ( | const BilinearFormContainer< Real > | frm1, |
| const Real | w | ||
| ) |
Simple multiplication from right
◆ operator*() [2/9]
|
inline |
Definition at line 246 of file vectorsMatrices.hh.
◆ operator*() [3/9]
| concepts::Array< typename Combtype< F, G >::type > concepts::operator* | ( | const concepts::Array< F > & | array, |
| const G & | val | ||
| ) |
◆ operator*() [4/9]
| Array< typename Combtype< F, G >::type > concepts::operator* | ( | const G & | val, |
| const Array< F > & | array | ||
| ) |
◆ operator*() [5/9]
| Cmplx concepts::operator* | ( | const Point< Cmplx, dim > & | a, |
| const Point< Real, dim > & | b | ||
| ) |
Definition at line 252 of file vectorsMatrices.hh.
◆ operator*() [6/9]
| Cmplx concepts::operator* | ( | const Point< Real, dim > & | a, |
| const Point< Cmplx, dim > & | b | ||
| ) |
Definition at line 261 of file vectorsMatrices.hh.
◆ operator*() [7/9]
|
inline |
Definition at line 240 of file vectorsMatrices.hh.
◆ operator*() [8/9]
| Sequence< typename Combtype< F, G >::type > concepts::operator* | ( | const Sequence< F > | seq1, |
| const G | factor | ||
| ) |
Definition at line 457 of file sequence.hh.
◆ operator*() [9/9]
| Sequence< typename Combtype< F, G >::type > concepts::operator* | ( | const Sequence< F > | seq1, |
| const Sequence< G > | seq2 | ||
| ) |
Definition at line 439 of file sequence.hh.
◆ operator+() [1/4]
| BilinearFormContainer< Real > concepts::operator+ | ( | const BilinearFormContainer< Real > | frm1, |
| const BilinearFormContainer< Real > | frm2 | ||
| ) |
Simple adding two element formulas by +-operator
◆ operator+() [2/4]
| ElementFormulaContainer< Real > concepts::operator+ | ( | const ElementFormulaContainer< Real > | frm1, |
| const ElementFormulaContainer< Real > | frm2 | ||
| ) |
Simple adding two element formulas by +-operator
◆ operator+() [3/4]
Simple adding two formulas by +-operator
concepts::ParsedFormula<> a("(x+y+z)"); concepts::ParsedFormula<> b("(x+y+2*z)"); std::cout << "a+b = " << a+b << std::endl;
◆ operator+() [4/4]
|
inline |
Definition at line 249 of file matrixIterator.hh.
◆ operator-() [1/3]
|
inline |
Definition at line 235 of file matrixIterator.hh.
◆ operator-() [2/3]
| BilinearFormContainer< Real > concepts::operator- | ( | const BilinearFormContainer< Real > | frm1, |
| const BilinearFormContainer< Real > | frm2 | ||
| ) |
Simple adding two element formulas by +-operator
◆ operator-() [3/3]
| ElementFormulaContainer< Real > concepts::operator- | ( | const ElementFormulaContainer< Real > | frm1, |
| const ElementFormulaContainer< Real > | frm2 | ||
| ) |
Simple subtracting two element formulas by "-"-operator
◆ operator/() [1/2]
| Sequence< typename Combtype< F, G >::type > concepts::operator/ | ( | const Sequence< F > | seq1, |
| const G | divisor | ||
| ) |
Definition at line 484 of file sequence.hh.
◆ operator/() [2/2]
| Sequence< typename Combtype< F, G >::type > concepts::operator/ | ( | const Sequence< F > | seq1, |
| const Sequence< G > | seq2 | ||
| ) |
Definition at line 470 of file sequence.hh.
◆ operator<() [1/3]
|
inline |
Definition at line 165 of file matrixIterator.hh.
◆ operator<() [2/3]
|
inline |
Definition at line 175 of file matrixIterator.hh.
◆ operator<() [3/3]
| bool concepts::operator< | ( | const Connector & | cntr_x, |
| const Connector & | cntr_y | ||
| ) |
<-operator sorted by the key, it could be useful for sorting, e.g. in std::set.
◆ operator<<() [1/18]
| ::std::ostream & concepts::operator<< | ( | ::std::ostream & | os, |
| TColumn< F > * | T | ||
| ) |
output-operator for pointer to TColumn, gives either 0 or TColumn itself
Definition at line 110 of file tmatrix.hh.
◆ operator<<() [2/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const AdaptiveAdjustP< dim > & | a | ||
| ) |
Definition at line 129 of file hpMethod.hh.
◆ operator<<() [3/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const AdaptiveControlP< dim, F > & | a | ||
| ) |
Definition at line 44 of file hpMethod.hh.
◆ operator<<() [4/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Array< F > & | o | ||
| ) |
◆ operator<<() [5/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const ElementMatrix< F > & | o | ||
| ) |
Definition at line 334 of file element.hh.
◆ operator<<() [6/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Graph< F > & | Value | ||
| ) |
◆ operator<<() [7/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const GraphVertex< F > & | Value | ||
| ) |
◆ operator<<() [8/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const HashedSparseMatrix< T > & | o | ||
| ) |
Definition at line 196 of file hashedSMatrix.hh.
◆ operator<<() [9/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Joiner< T, nlnk > & | j | ||
| ) |
Definition at line 161 of file scannerConnectors.hh.
◆ operator<<() [10/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Mapping< F, DimY, DimX > & | m | ||
| ) |
Definition at line 609 of file vectorsMatrices.hh.
◆ operator<<() [11/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Orders< number > & | o | ||
| ) |
Definition at line 43 of file karniadakis.hh.
◆ operator<<() [12/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const Point< F, dim > & | p | ||
| ) |
Definition at line 213 of file vectorsMatrices.hh.
◆ operator<<() [13/18]
|
protected |
Definition at line 79 of file outputOperator.hh.
◆ operator<<() [14/18]
|
protected |
Definition at line 90 of file outputOperator.hh.
◆ operator<<() [15/18]
|
protected |
Definition at line 72 of file outputOperator.hh.
◆ operator<<() [16/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const std::unique_ptr< F > & | p | ||
| ) |
Definition at line 54 of file outputOperator.hh.
◆ operator<<() [17/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| const std::vector< T * > & | field | ||
| ) |
Definition at line 140 of file meshImport.hh.
◆ operator<<() [18/18]
| std::ostream & concepts::operator<< | ( | std::ostream & | os, |
| std::unique_ptr< F > & | a | ||
| ) |
◆ operator<=() [1/2]
|
inline |
Definition at line 201 of file matrixIterator.hh.
◆ operator<=() [2/2]
|
inline |
Definition at line 209 of file matrixIterator.hh.
◆ operator==() [1/6]
|
inline |
Definition at line 130 of file matrixIterator.hh.
◆ operator==() [2/6]
|
inline |
Definition at line 140 of file matrixIterator.hh.
◆ operator==() [3/6]
|
inline |
◆ operator==() [4/6]
|
inline |
◆ operator==() [5/6]
|
inline |
Definition at line 231 of file vectorsMatrices.hh.
◆ operator==() [6/6]
|
inline |
◆ operator>() [1/2]
|
inline |
Definition at line 186 of file matrixIterator.hh.
◆ operator>() [2/2]
|
inline |
Definition at line 194 of file matrixIterator.hh.
◆ operator>=() [1/2]
|
inline |
Definition at line 218 of file matrixIterator.hh.
◆ operator>=() [2/2]
|
inline |
Definition at line 226 of file matrixIterator.hh.
◆ operator>>() [1/2]
| std::istream & concepts::operator>> | ( | std::istream & | is, |
| BaseSequence< F > & | seq | ||
| ) |
Definition at line 133 of file sequence.hh.
◆ operator>>() [2/2]
| std::istream & concepts::operator>> | ( | std::istream & | is, |
| BaseSet< F > & | set | ||
| ) |
◆ outputMatlab() [1/5]
|
inline |
Function for output of ElementMatrix to Matlab
example use: outputMatlab(std::cout << "M = ",M) << std::endl;
Definition at line 88 of file outputMatlab.hh.
◆ outputMatlab() [2/5]
| std::ostream & concepts::outputMatlab | ( | std::ostream & | os, |
| const std::complex< T > & | val | ||
| ) |
Definition at line 36 of file outputMatlab.hh.
◆ outputMatlab() [3/5]
| std::ostream & concepts::outputMatlab | ( | std::ostream & | os, |
| const T & | val | ||
| ) |
Function for output of basic types to matlab
example use: outputMatlab(std::cout << "x = ",x) << std::endl;
Definition at line 30 of file outputMatlab.hh.
◆ outputMatlab() [4/5]
Function for output of T-Matrix to Matlab.
example use: outputMatlab(std::cout << "T = ",T) << std::endl;
Definition at line 22 of file outputMatlab.hh.
◆ outputMatlab() [5/5]
|
inline |
Function for output of T-Matrix base class to Matlab.
example use: outputMatlab(std::cout << "T = ",T) << std::endl;
Definition at line 73 of file outputMatlab.hh.
◆ pointerOutput() [1/4]
◆ pointerOutput() [2/4]
Definition at line 16 of file pointerOutput.hh.
◆ pointerOutput() [3/4]
Definition at line 21 of file pointerOutput.hh.
◆ pointerOutput() [4/4]
Definition at line 27 of file pointerOutput.hh.
◆ prodTranspose() [1/2]
Definition at line 50 of file operations.hh.
◆ prodTranspose() [2/2]
Definition at line 46 of file operations.hh.
◆ product() [1/2]
Definition at line 41 of file operations.hh.
◆ product() [2/2]
Definition at line 36 of file operations.hh.
◆ quadratureWeightTensor() [1/2]
| Array< Real > concepts::quadratureWeightTensor | ( | const Array< QuadratureRule1d * > & | ArrayQuad1D | ) |
Computes a multi-dimensional quadrature weight tensor
- Parameters
-
ArrayQuad1D pointers to 1D quadratures
◆ quadratureWeightTensor() [2/2]
| Real concepts::quadratureWeightTensor | ( | const Array< QuadratureRule1d * > & | ArrayQuad1D, |
| const Array< int > & | Index | ||
| ) |
Compute a quadrature weight tensor at a partical index point
- Parameters
-
ArrayQuad1D pointers to 1D quadratures Index index to compute
◆ ReadEigenValuesFromFile()
| concepts::Sequence< Cmplx > concepts::ReadEigenValuesFromFile | ( | const int | NDtN_given, |
| const std::string | Filename | ||
| ) |
Definition at line 762 of file DtNmap2D_visc.hh.
◆ realSeqFromStringWithPower()
Converts a string to a sequence of real numbers, where a power may be allowed to express, e.g., negative powers of 2.
The string "1.0 2e-8 2p-2" results in Sequence(1, 2e-08, 0.25)
◆ securePointer() [1/2]
Definition at line 265 of file matrixIterator.hh.
◆ securePointer() [2/2]
Templated function, which prevent a pointer to a temporary value got from constant matrices with index operator .
Definition at line 262 of file matrixIterator.hh.
◆ sgn()
Definition at line 37 of file DtNmap2D_visc.hh.
◆ sparseLineToArrays()
◆ splitString()
| std::vector< std::string > concepts::splitString | ( | const std::string | text, |
| const std::string | separators | ||
| ) |
Split the string text string into words, where the separation token are included in separators.
◆ splitStringByComma()
| std::vector< std::string > concepts::splitStringByComma | ( | const std::string | text | ) |
Split a strings in words separated by commas while respecting the bracket hierachies.
It splits "Ellipse(1.0, 4), Circle()" into "Ellipse(1.0, 4)" and "Circle()".
◆ splitStringNameParams()
| std::vector< std::string > concepts::splitStringNameParams | ( | const std::string | text | ) |
Split a string like "Ellipse(1.0, 4)" into "Ellipse", "1.0", "4".
◆ sqr()
Definition at line 27 of file DtNmap2D_visc.hh.
◆ storeDenseMatrixToMatlab() [1/2]
| bool concepts::storeDenseMatrixToMatlab | ( | F & | matrix, |
| const uint | nofRows, | ||
| const uint | nofCols, | ||
| const std::string | filename, | ||
| std::string | name = "", |
||
| bool | append = false |
||
| ) |
Stores a matrix to the matlab file filename as dense matrix name. If append is false, overwrite old file, if already existed.
Its applicable for any concepts::Matrix and for concepts::ElementMatrix as well.
- Returns
- true if the writing to the file was successfull
Definition at line 32 of file outputMatlab.hh.
◆ storeDenseMatrixToMatlab() [2/2]
| void concepts::storeDenseMatrixToMatlab | ( | F & | matrix, |
| const uint | nofRows, | ||
| const uint | nofCols, | ||
| std::ostream & | ofs, | ||
| std::string | name = "" |
||
| ) |
Writes a matrix to the stream ofs as dense matrix name in Matlab format.
Its applicable for any concepts::Matrix and for concepts::ElementMatrix as well.
- Returns
- true if the writing to the file was successfull
Definition at line 62 of file outputMatlab.hh.
◆ storeSparseMatrixToOctave()
| void concepts::storeSparseMatrixToOctave | ( | SparseMatrix< F > & | matrix, |
| std::ostream & | ofs, | ||
| std::string | name = "" |
||
| ) |
Writes a matrix to the stream ofs as dense matrix name in Octave format (older version don't have sparse matrix format).
Its applicable for any concepts::Matrix and for concepts::HashedSMatrix as well.
- Returns
- true if the writing to the file was successfull
Definition at line 98 of file outputMatlab.hh.
◆ stringSubs()
| std::string concepts::stringSubs | ( | const std::string | str, |
| const std::string | var, | ||
| F | value | ||
| ) |
Substitute all occurances of a substring var of a string str by value which may be for example a real or another string.
Definition at line 81 of file stringFunc.hh.
◆ transpose() [1/2]
Definition at line 58 of file operations.hh.
◆ transpose() [2/2]
Definition at line 54 of file operations.hh.
◆ typeOf()
| std::string concepts::typeOf | ( | const T & | t | ) |
◆ uintSeqSets()
| Sequence< concepts::Set< uint > > concepts::uintSeqSets | ( | const std::string | s | ) |
Converts a string to a sequence of sets of uint.
The numbers in each set are separated by a comma, whereas the differents sets are separated by a semicolon.
The string "1, 2, 3; 4" results in Sequence(Set(1,2,3), Set(4))
◆ visc_ell_fast()
| Cmplx concepts::visc_ell_fast | ( | const Cmplx | lambda, |
| const Real | nu, | ||
| const Real | omega, | ||
| const Real | rho0 | ||
| ) |
Definition at line 44 of file DtNmap2D_visc.hh.
◆ visc_ell_slow()
Generated on Wed Sep 13 2023 21:06:30 for Concepts by

![\[g_{j,f}\]](form_695.png)
![\[g_{j,s}\]](form_696.png)
![\[\lambda_{j,f}\]](form_693.png)
![\[\lambda_{j,s}\]](form_694.png)