concepts::BesselY< n > Class Template Reference

#include <bessel.hh>

Inheritance diagram for concepts::BesselY< n >:

Public Types
typedef Real	value_type
typedef Realtype< Real >::type	G

Public Member Functions
	BesselY (const Real m=1.0, const Real r0=0.0)
	Constructor.
	BesselY (const Real m, const Real3d r0)
virtual Real	operator() (const Real p, const Real t=0.0) const
	Bessel function.
virtual Real	operator() (const Real2d &p, const Real t=0.0) const
virtual Real	operator() (const Real3d &p, const Real t=0.0) const
Real	derivative (const Real p)
	Derivative of Bessel function.
Real	derivative (const Real2d &p)
Real	derivative (const Real3d &p)
virtual BesselY< n > *	clone () const
	Virtual copy constructor.
virtual F	operator() (const ElementWithCell< G > &elm, const Real p, const Real t=0.0) const
virtual F	operator() (const ElementWithCell< G > &elm, const Real2d &p, const Real t=0.0) const
virtual F	operator() (const ElementWithCell< G > &elm, const Real3d &p, const Real t=0.0) const
virtual F	operator() (const ElementWithCell< concepts::Realtype< F >::type > &elm, const Real p, const Real t=0.0) const=0
virtual F	operator() (const ElementWithCell< concepts::Realtype< F >::type > &elm, const Real2d &p, const Real t=0.0) const=0
virtual F	operator() (const ElementWithCell< concepts::Realtype< F >::type > &elm, const Real3d &p, const Real t=0.0) const=0
virtual const F &	dflt_value () const
	Gives default value.
virtual F &	dflt_value ()
	Gives default value.
virtual Real	operator() (const Connector &cntr, const Real p, const Real t=0.0) const
virtual Real	operator() (const Connector &cntr, const Real2d &p, const Real t=0.0) const
virtual Real	operator() (const Connector &cntr, const Real3d &p, const Real t=0.0) const

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

template<int n>
class concepts::BesselY< n >

Class for evaluating the Bessel function of second kind.

A center r0 and a shortening factor n can be given to evaluate

, where is the distance from the origin.

Author

(C) Copr. 1988-92 Numerical Recipes Software. Abramowitz and Stegun. Handbook of Mathematical Functions.

Definition at line 208 of file bessel.hh.

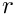
Member Typedef Documentation

G

typedef Realtype<Real >::type concepts::Formula< Real >::G

inherited

Definition at line 37 of file formula.hh.

value_type

typedef Real concepts::Formula< Real >::value_type

inherited

Definition at line 36 of file formula.hh.

Constructor & Destructor Documentation

BesselY() [1/2]

template<int n>

concepts::BesselY< n >::BesselY ( const Real  m = 1.0, const Real  r0 = 0.0  )

inline

Constructor.

Definition at line 211 of file bessel.hh.

BesselY() [2/2]

template<int n>

concepts::BesselY< n >::BesselY ( const Real  m, const Real3d  r0  )

inline

Definition at line 213 of file bessel.hh.

Member Function Documentation

clone()

template<int n>

virtual BesselY< n > * concepts::BesselY< n >::clone ( ) const

inlinevirtual

Virtual copy constructor.

Implements concepts::Formula< Real >.

Definition at line 224 of file bessel.hh.

derivative() [1/3]

template<int n>

Real concepts::BesselY< n >::derivative

(

const Real

p

)

Derivative of Bessel function.

Definition at line 252 of file bessel.hh.

derivative() [2/3]

template<int n>

Real concepts::BesselY< n >::derivative

(

const Real2d &

p

)

Definition at line 258 of file bessel.hh.

derivative() [3/3]

template<int n>

Real concepts::BesselY< n >::derivative

(

const Real3d &

p

)

Definition at line 264 of file bessel.hh.

dflt_value() [1/2]

template<typename F >

virtual F & concepts::PiecewiseFormulaBase< F >::dflt_value ( )

inlinevirtualinherited

Gives default value.

Definition at line 83 of file piecewiseFormula.hh.

dflt_value() [2/2]

template<typename F >

virtual const F & concepts::PiecewiseFormulaBase< F >::dflt_value ( ) const

inlinevirtualinherited

Gives default value.

Definition at line 81 of file piecewiseFormula.hh.

info()

template<int n>

std::ostream & concepts::BesselY< n >::info ( std::ostream &  os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::PiecewiseFormulaBase< F >.

Definition at line 270 of file bessel.hh.

operator()() [1/12]

virtual Real concepts::Formula< Real >::operator() ( const Connector &  cntr, const Real  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Convenience implementation, that by default ignores its elm param.

Implements concepts::PiecewiseFormulaBase< F >.

Definition at line 53 of file formula.hh.

operator()() [2/12]

virtual Real concepts::Formula< Real >::operator() ( const Connector &  cntr, const Real2d &  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Implements concepts::PiecewiseFormulaBase< F >.

Definition at line 56 of file formula.hh.

operator()() [3/12]

virtual Real concepts::Formula< Real >::operator() ( const Connector &  cntr, const Real3d &  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Implements concepts::PiecewiseFormulaBase< F >.

Definition at line 59 of file formula.hh.

operator()() [4/12]

virtual F concepts::ElementFormula< F, concepts::Realtype< F >::type >::operator() ( const ElementWithCell< concepts::Realtype< F >::type > &  elm, const Real  p, const Real  t = 0.0  ) const

pure virtualinherited

Evaluates the formula.

Parameters

elm	Element
p	Point in space in local element coordinates
t	Point in time

operator()() [5/12]

virtual F concepts::ElementFormula< F, concepts::Realtype< F >::type >::operator() ( const ElementWithCell< concepts::Realtype< F >::type > &  elm, const Real2d &  p, const Real  t = 0.0  ) const

pure virtualinherited

Evaluates the formula.

Parameters

elm	Element
p	Point in space in local element coordinates
t	Point in time

operator()() [6/12]

virtual F concepts::ElementFormula< F, concepts::Realtype< F >::type >::operator() ( const ElementWithCell< concepts::Realtype< F >::type > &  elm, const Real3d &  p, const Real  t = 0.0  ) const

pure virtualinherited

Evaluates the formula.

Parameters

elm	Element
p	Point in space in local element coordinates
t	Point in time

operator()() [7/12]

template<typename F >

virtual F concepts::PiecewiseFormulaBase< F >::operator() ( const ElementWithCell< G > &  elm, const Real  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Definition at line 52 of file piecewiseFormula.hh.

operator()() [8/12]

template<typename F >

virtual F concepts::PiecewiseFormulaBase< F >::operator() ( const ElementWithCell< G > &  elm, const Real2d &  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Definition at line 57 of file piecewiseFormula.hh.

operator()() [9/12]

template<typename F >

virtual F concepts::PiecewiseFormulaBase< F >::operator() ( const ElementWithCell< G > &  elm, const Real3d &  p, const Real  t = 0.0  ) const

inlinevirtualinherited

Definition at line 63 of file piecewiseFormula.hh.

operator()() [10/12]

template<int n>

Real concepts::BesselY< n >::operator() ( const Real  p, const Real  t = 0.0  ) const

virtual

Bessel function.

Implements concepts::Formula< Real >.

Definition at line 237 of file bessel.hh.

operator()() [11/12]

template<int n>

Real concepts::BesselY< n >::operator() ( const Real2d &  p, const Real  t = 0.0  ) const

virtual

Implements concepts::Formula< Real >.

Definition at line 242 of file bessel.hh.

operator()() [12/12]

template<int n>

Real concepts::BesselY< n >::operator() ( const Real3d &  p, const Real  t = 0.0  ) const

virtual

Implements concepts::Formula< Real >.

Definition at line 247 of file bessel.hh.

---

The documentation for this class was generated from the following file:

• formula/bessel.hh