concepts::IntegrationCell Class Reference

#include <integral.hh>

Inheritance diagram for concepts::IntegrationCell:

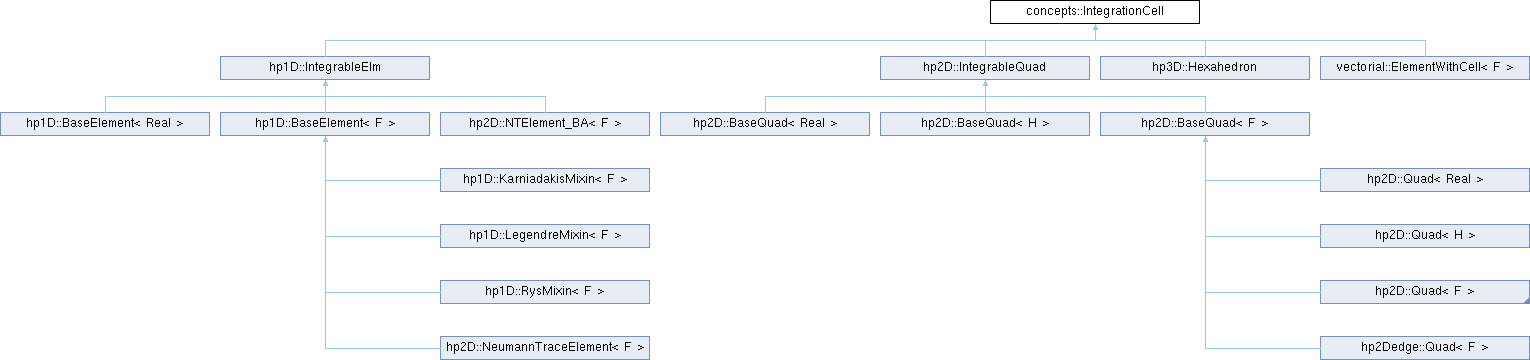
Classes
struct	intPoint

Public Types
enum	intFormType { ZERO , ONE , TWO , THREE }

Public Member Functions
	IntegrationCell ()
	Constructor.
virtual bool	quadraturePoint (uint i, intPoint &p, intFormType form=ZERO, bool localCoord=false) const =0

Detailed Description

Cell over which can be integrated.

For that a single method exists, which delivers quadrature points, weights and a term from mapping. The method has to be implemented in the derived classes.

Author

Kersten Schmidt, 2005

Definition at line 24 of file integral.hh.

Member Enumeration Documentation

intFormType

enum concepts::IntegrationCell::intFormType

Integration form, which determines terms coming from integration over reference element

Definition at line 29 of file integral.hh.

Constructor & Destructor Documentation

IntegrationCell()

concepts::IntegrationCell::IntegrationCell ( )

inline

Constructor.

Definition at line 40 of file integral.hh.

~IntegrationCell()

virtual concepts::IntegrationCell::~IntegrationCell ( )

inlinevirtual

Definition at line 41 of file integral.hh.

Member Function Documentation

quadraturePoint()

virtual bool concepts::IntegrationCell::quadraturePoint ( uint  i, intPoint &  p, intFormType  form = ZERO, bool  localCoord = false  ) const

pure virtual

Delivers a quadrature point.

Quadrature point consists of coordinates (for evaluation of formulas) and intermediate data, consisting of the weight and term coming from mapping.

Returns false, if the number of quadrature points is overstepped.

Parameters

i	number of quadrature point
intPoint	data given back
form	Integration form
localCoord	If true, local coordinates are returned. Else physical coordinates.

Implemented in hp3D::Hexahedron, vectorial::ElementWithCell< F >, hp1D::IntegrableElm, and hp2D::IntegrableQuad.

---

The documentation for this class was generated from the following file:

• geometry/integral.hh