hp1D::LevelRieszElement Class Reference

#include <levelRieszElement.hh>

Inheritance diagram for hp1D::LevelRieszElement:

Public Member Functions
	LevelRieszElement (const hp2D::Element< Real > &elm, const concepts::ElementFormulaContainer< Real > &levelFunction, const concepts::ElementFormulaContainer< Real2d > &levelFunctionGrad, const concepts::ElementFormulaContainer< Real > &observable)
	~LevelRieszElement ()
void	operator() (const concepts::Element< Real > &elm, concepts::ElementMatrix< Real > &em) const
virtual void	operator() (const Element< typename Realtype< concepts::Real >::type > &elm, ElementMatrix< concepts::Real > &em) const=0

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

This class creates a linearform corresponding to the local contribution of one cell to the integral:

,

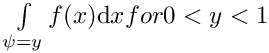
where \psi is a given 2D-function (must take values between 0 and 1 !) and f the function to be integrated.

These integrals, called geometric coefficients, are computed for all y in [0,1] via a Galerkin-projection on a polynomial space. As polynomials spaces one can choose the space of orthonormal Legendre-polynomials (hp1D::hpAdaptiveSpaceL2) or the space of Karniadakis-polynomials (hp1D::Space).

Author

Lukas Drescher, 2015, Felix Baumann 2017

Definition at line 34 of file levelRieszElement.hh.

Constructor & Destructor Documentation

LevelRieszElement()

hp1D::LevelRieszElement::LevelRieszElement	(	const hp2D::Element< Real > &	elm,
		const concepts::ElementFormulaContainer< Real > &	levelFunction,
		const concepts::ElementFormulaContainer< Real2d > &	levelFunctionGrad,
		const concepts::ElementFormulaContainer< Real > &	observable
	)

Constructor

Parameters

elm	a 2D-element
levelFunction	levelset function. must take values in [0,1]
levelFunctionGrad	gradient of levelset function
observable	integrand over level sets of levelFunction

~LevelRieszElement()

hp1D::LevelRieszElement::~LevelRieszElement

(

)

Destructor

Member Function Documentation

info()

virtual std::ostream & hp1D::LevelRieszElement::info ( std::ostream &  os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::LinearForm< concepts::Real >.

operator()()

virtual void concepts::LinearForm< concepts::Real , typename Realtype<concepts::Real >::type >::operator() ( const Element< typename Realtype<concepts::Real >::type > &  elm, ElementMatrix< concepts::Real > &  em  ) const

pure virtualinherited

Computes the element contribution to the function.

Parameters

elm	Element on which the computations should be performed
em	The local matrix

---

The documentation for this class was generated from the following file:

• levelSets/levelRieszElement.hh