You are here: Concepts>Concepts Web>Class documentation
Class documentation of Concepts
Loading...
Searching...
No Matches
hp3D::LinearFormHelper_1< F > Class Template Reference
#include <linearFormHelper.hh>
Inheritance diagram for hp3D::LinearFormHelper_1< F >:

Public Member Functions | |
| LinearFormHelper_1 (const concepts::ElementFormulaContainer< F > frm1, const concepts::ElementFormulaContainer< F > frm2, const concepts::ElementFormulaContainer< F > frm3) | |
| LinearFormHelper_1 (const concepts::ElementFormulaContainer< concepts::Point< F, 3 > > frm) | |
Protected Member Functions | |
| void | computeIntermediate_ (const Hexahedron &elm) const |
Protected Attributes | |
| ArrayElementFormula< concepts::Point< F, 3 > > | intermediateVector_ |
| concepts::ElementFormulaContainer< concepts::Point< F, 3 > > | frm_ |
| ElementFormula. | |
Detailed Description
template<class F>
class hp3D::LinearFormHelper_1< F >
class hp3D::LinearFormHelper_1< F >
Helper class for linearforms l(v), where v is a one form
![\[\displaystyle l(v)
= \int\limits_K \underline{f}(x)^\top\underline{v}\,dx
= \int\limits_{\hat{K}} \underline{f}(F_K(\xi))^\top J^{-1}
\hat{\underline{v}}\,\circ F_K^{-1} \det J\,d\xi
= \int\limits_{\hat{K}} \underline{f}(F_K(\xi))^\top
\mbox{adj}(J)^\top\hat{\underline{v}}\,\circ F_K^{-1}\,d\xi\]](form_537.png)
Here, 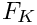
![$\hat{K} = [0,1]^2$](form_536.png)
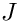
Precomputes intermediate data for element matrix computation, this is
![\[\underline{f}(F_K(\xi))^\top \mbox{adj}(J)^\top
= \underline{f}(F_K(\xi))^\top J^{-\top}\det J,\]](form_538.png)
which is stored as a single vector intermediateVector_ for each quadrature point.
The class can be used as well for bilinear forms a(u,v) where u is a 0-form and v is a 1-form. One example is the bilinear form hp2D::Advection
![\[
\int\limits_{K} \underline{k}^\top u \; \nabla{v} \; d\xi
= \int\limits_{\hat{K}} \underline{k}^\top \hat{u} \;
J^{-\top}\;\nabla{\hat{v}} \;|\det J| \; d\hat{\xi}.
\]](form_489.png)
Definition at line 65 of file linearFormHelper.hh.
Member Function Documentation
◆ computeIntermediate_()
template<class F >
|
protected |
Compute the intermediate data for element matrix computation
This method is important for the derivated linear forms.
Member Data Documentation
◆ frm_
template<class F >
|
protected |
ElementFormula.
Definition at line 88 of file linearFormHelper.hh.
◆ intermediateVector_
template<class F >
|
mutableprotected |
The documentation for this class was generated from the following file:
- hp3D/linearFormHelper.hh
Generated on Wed Sep 13 2023 21:06:56 for Concepts by

![\[\underline{f}(F_K(\xi))^\top \mbox{adj}(J)^\top\]](form_542.png)