You are here: Concepts>Concepts Web>Class documentation

Class documentation of Concepts

Loading...
Searching...
No Matches
Public Member Functions | Protected Member Functions | Protected Attributes | List of all members
hp2D::Advection< F > Class Template Referenceabstract

#include <bf_advection.hh>

Inheritance diagram for hp2D::Advection< F >:
concepts::BilinearForm< F, G > hp2D::LinearFormHelper_1< F > concepts::Cloneable concepts::OutputOperator

Public Member Functions

 Advection (const concepts::ElementFormulaContainer< F > frm1, const concepts::ElementFormulaContainer< F > frm2)
 
 Advection (const concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm)
 
virtual Advection< F > * clone () const
 
virtual void operator() (const concepts::Element< Real > &elmX, const concepts::Element< Real > &elmY, concepts::ElementMatrix< F > &em) const
 
virtual void operator() (const Element< G > &elmX, const Element< G > &elmY, ElementMatrix< F > &em) const =0
 
virtual void operator() (const Element< G > &elmX, const Element< G > &elmY, ElementMatrix< F > &em, const ElementPair< G > &ep) const
 

Protected Member Functions

virtual std::ostream & info (std::ostream &os) const
 Returns information in an output stream.
 
void computeIntermediate_ (const BaseQuad< concepts::Real > &elm) const
 

Protected Attributes

ArrayElementFormula< concepts::Point< F, 2 > > intermediateVector_
 
concepts::ElementFormulaContainer< concepts::Point< F, 2 > > frm_
 ElementFormula.
 

Detailed Description

template<class F = Real>
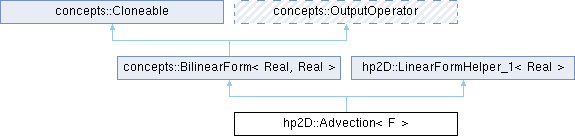
class hp2D::Advection< F >

A function class to calculate element matrices for the bilinear form

\[ \int\limits_{K} \underline{k}^\top u \; \nabla{v} \; d\xi = \int\limits_{\hat{K}} \underline{k}^\top \hat{u} \; J^{-\top}\;\nabla{\hat{v}} \;|\det J| \; d\hat{\xi}. \]

Here k is an arbitrary vector-valued function with coefficients. For some k, the resulting matrix might be singular, e.g. k=[0,0].

It can be used for the advection term in flow problems or for the asymmetric part of the bilinear form for photonic crystals using periodic boundary conditions.

Test:
for tests see app-bholger/test_*
Author
Holger Brandsmeier, 2008

Definition at line 72 of file bf_advection.hh.

Constructor & Destructor Documentation

◆ Advection() [1/2]

template<class F = Real>
hp2D::Advection< F >::Advection ( const concepts::ElementFormulaContainer< F >  frm1,
const concepts::ElementFormulaContainer< F >  frm2 
)
inline

Definition at line 76 of file bf_advection.hh.

◆ Advection() [2/2]

template<class F = Real>
hp2D::Advection< F >::Advection ( const concepts::ElementFormulaContainer< concepts::Point< F, 2 > >  frm)
inline

Definition at line 81 of file bf_advection.hh.

◆ ~Advection()

template<class F = Real>
virtual hp2D::Advection< F >::~Advection ( )
inlinevirtual

Definition at line 86 of file bf_advection.hh.

Member Function Documentation

◆ clone()

template<class F = Real>
virtual Advection< F > * hp2D::Advection< F >::clone ( ) const
inlinevirtual

Virtual constructor. Returns a pointer to a copy of itself. The caller is responsible to destroy this copy.

Implements concepts::BilinearForm< F, G >.

Definition at line 88 of file bf_advection.hh.

◆ computeIntermediate_()

template<class F >
void hp2D::LinearFormHelper_1< F >::computeIntermediate_ ( const BaseQuad< concepts::Real > &  elm) const
protectedinherited

Compute the intermediate data for element matrix computation

This method is important for the derivated linear forms.

◆ info()

template<class F = Real>
virtual std::ostream & hp2D::Advection< F >::info ( std::ostream &  os) const
protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::BilinearForm< F, G >.

◆ operator()() [1/2]

template<class F , class G = typename Realtype<F>::type>
virtual void concepts::BilinearForm< F, G >::operator() ( const Element< G > &  elmX,
const Element< G > &  elmY,
ElementMatrix< F > &  em 
) const
pure virtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em.

Postcondition
The returned matrix em has the correct size.
Parameters
elmXLeft element (test functions)
elmYRight element (trial functions)
emReturn element matrix

Implemented in vectorial::BilinearForm< F, G >, concepts::BilinearFormLiCo< F, G >, concepts::BilinearFormContainer< F, G >, concepts::BilinearF_Sum< F, H, J, G >, and concepts::BilinearF_W< F, H, J, G >.

◆ operator()() [2/2]

template<class F , class G = typename Realtype<F>::type>
virtual void concepts::BilinearForm< F, G >::operator() ( const Element< G > &  elmX,
const Element< G > &  elmY,
ElementMatrix< F > &  em,
const ElementPair< G > &  ep 
) const
inlinevirtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em. If this method is not reimplemented in a derived class, the default behaviour is to call the application operator without ep.

Postcondition
The returned matrix em has the correct size.
Parameters
elmXLeft element
elmYRight element
emReturn element matrix
epElement pair holding more information on the pair elmX and elmY

Reimplemented in vectorial::BilinearForm< F, G >.

Definition at line 57 of file bilinearForm.hh.

Member Data Documentation

◆ frm_

template<class F >
concepts::ElementFormulaContainer<concepts::Point<F, 2> > hp2D::LinearFormHelper_1< F >::frm_
protectedinherited

ElementFormula.

Definition at line 139 of file linearFormHelper.hh.

◆ intermediateVector_

template<class F >
ArrayElementFormula<concepts::Point<F,2> > hp2D::LinearFormHelper_1< F >::intermediateVector_
mutableprotectedinherited

Intermediate vector (on each quadrature point)

\[\underline{f}(F_K(\xi))^\top \mbox{adj}(J)^\top\]

Definition at line 136 of file linearFormHelper.hh.

The documentation for this class was generated from the following file:
Generated on Wed Sep 13 2023 21:06:52 for Concepts by doxygen 1.9.8