#include <cgUzawa.hh>

Inheritance diagram for vectorial::CGUzawa:

Public Types
typedef Real	type
	Type of data, e.g. matrix entries.

typedef Realtype< Real >::type	r_type
	Real type of data type.

typedef Cmplxtype< Real >::type	c_type
	Real type of data type.

Public Member Functions
	CGUzawa (concepts::Operator< Real > &A, concepts::Operator< Real > &B, concepts::Operator< Real > &Bt, concepts::Operator< Real > &C, concepts::Operator< Real > &Ai, Real maxeps, int maxit=0, uint relres=false)

virtual void	operator() (const concepts::Function< Real > &fncY, concepts::Function< Real > &fncX)

void	operator() (const concepts::Vector< Real > &fncY, concepts::Vector< Real > &fncX)

uint	iterations () const

Real	epsilon () const

virtual void	operator() (const Function< r_type > &fncY, Function< Real > &fncX)

virtual void	operator() (const Function< c_type > &fncY, Function< c_type > &fncX)

virtual void	operator() ()

virtual const uint	dimX () const

virtual const uint	dimY () const

virtual void	show_messages ()

Protected Member Functions
std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Protected Attributes
uint	dimX_
	Dimension of image space and the source space.

uint	dimY_

Detailed Description

Uzawa algorithm with conjugate directions for generalized saddle point problems.

$\left(\begin{array}{lr}A&B\\B^{\top}&-C\end{array}\right) \left(\begin{array}{c}U\\P\end{array}\right) = \left(\begin{array}{c}L_u\\L_p\end{array}\right)$

A has to be symmetric and positive definite, C has to be symmetric and positive semidefinite, and B has to satisfy the discrete inf-sup-condition.

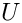
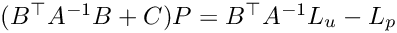
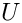
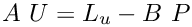
The main idea is to eliminate from the above equation, resulting in the equation $(B^{\top} A^{-1} B + C)P = B^{\top} A^{-1}L_u - L_p$ . This reduced system is solved with conjugate gradients. The action of A^-1 is a suitable solver that has to be provided at construction time. Then, is obtained from $A \ U = L_u - B \ P$ . See [1] for more details.

The class is an operator on a vectorial::Space consisting of two spaces, say spc1 and spc2. A is spc1->spc1, B is spc2->spc1 and C is spc2->spc2. The entire vectorial space has to be provided at construction time.

Constructing an object of this class does not solve the given system. Use the application operator to solve the system. If you want to specify a starting vector for the cg iterations, set fncX before calling the application operator to this starting value. fncX also holds the result after the solve.

The application operator throws NoConvergence if the desired residual maxeps is not reached within the given number of iterations maxit.

See also: D. Braess: Finite Elemente: Theorie, schnelle Löser und Anwendungen in der Elastitzitätstheorie. Springer, Berlin, 1997.

Definition at line 55 of file cgUzawa.hh.

Member Typedef Documentation

◆ c_type

typedef Cmplxtype<Real >::type concepts::Operator< Real >::c_type

inherited

Real type of data type.

Definition at line 49 of file compositions.hh.

◆ r_type

typedef Realtype<Real >::type concepts::Operator< Real >::r_type

inherited

Real type of data type.

Definition at line 47 of file compositions.hh.

◆ type

typedef Real concepts::Operator< Real >::type

inherited

Type of data, e.g. matrix entries.

Definition at line 45 of file compositions.hh.

Constructor & Destructor Documentation

◆ CGUzawa()

vectorial::CGUzawa::CGUzawa	(	concepts::Operator< Real > &	A,
		concepts::Operator< Real > &	B,
		concepts::Operator< Real > &	Bt,
		concepts::Operator< Real > &	C,
		concepts::Operator< Real > &	Ai,
		Real	maxeps,
		int	maxit = `0`,
		uint	relres = `false`
	)

Constructor.

Parameters

A	Upper left submatrix
B	Upper right submatrix
Bt	Lower left submatrix
C	Lower right submatrix
Ai	Solver for A
spc	Entire vectorial space
maxeps	Maximal residual
maxit	Maximal number of iterations
relres	Relative residual

Member Function Documentation

◆ dimX()

virtual const uint concepts::Operator< Real >::dimX ( ) const

inlinevirtualinherited

Returns the size of the image space of the operator (number of rows of the corresponding matrix)

Definition at line 93 of file compositions.hh.

◆ dimY()

virtual const uint concepts::Operator< Real >::dimY ( ) const

inlinevirtualinherited

Returns the size of the source space of the operator (number of columns of the corresponding matrix)

Definition at line 98 of file compositions.hh.

◆ epsilon()

Real vectorial::CGUzawa::epsilon ( ) const

inline

Returns the residual. Calling this method makes only sense after a linear system has been solved.

Definition at line 86 of file cgUzawa.hh.

◆ info()

std::ostream & vectorial::CGUzawa::info ( std::ostream & os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::Operator< Real >.

◆ iterations()

uint vectorial::CGUzawa::iterations ( ) const

inline

Returns the number of (outer) iterations. Calling this method makes only sense after a linear system has been solved.

Definition at line 81 of file cgUzawa.hh.

◆ operator()() [1/3]

virtual void concepts::Operator< Real >::operator() ( )

virtualinherited

Application operator without argument

◆ operator()() [2/3]

virtual void concepts::Operator< Real >::operator()	(	const Function< c_type > &	fncY,
		Function< c_type > &	fncX
	)

virtualinherited

Application operator for complex function fncY.

Computes fncX = A(fncY) where A is this operator. fncX becomes complex.

In derived classes its enough to implement the operator() for complex Operator's. If a real counterpart is not implemented, the function fncY is splitted into real and imaginary part and the application operator for real functions is called for each. Then the result is combined.

If in a derived class the operator() for complex Operator's is not implemented, a exception is thrown from here.

◆ operator()() [3/3]

virtual void concepts::Operator< Real >::operator()	(	const Function< r_type > &	fncY,
		Function< Real > &	fncX
	)

virtualinherited

Application operator for real function fncY.

Computes fncX = A(fncY) where A is this operator.

fncX becomes the type of the operator, for real data it becomes real, for complex data it becomes complex.

In derived classes its enough to implement the operator() for real Operator's. If a complex counterpart is not implemented, the function fncY is transformed to a complex function and then the application operator for complex functions is called.

If in a derived class the operator() for real Operator's is not implemented, a exception is thrown from here.

◆ show_messages()

virtual void concepts::Operator< Real >::show_messages ( )

inlinevirtualinherited

Definition at line 100 of file compositions.hh.

Member Data Documentation

◆ dimX_

uint concepts::Operator< Real >::dimX_

protectedinherited

Dimension of image space and the source space.

Definition at line 104 of file compositions.hh.

◆ dimY_

uint concepts::Operator< Real >::dimY_

protectedinherited

Definition at line 104 of file compositions.hh.

The documentation for this class was generated from the following file:

vectorial/cgUzawa.hh

Class documentation of Concepts

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Member Typedef Documentation

◆ c_type

◆ r_type

◆ type

Constructor & Destructor Documentation

◆ CGUzawa()

Member Function Documentation

◆ dimX()

◆ dimY()

◆ epsilon()

◆ info()

◆ iterations()

◆ operator()() [1/3]

◆ operator()() [2/3]

◆ operator()() [3/3]

◆ show_messages()

Member Data Documentation

◆ dimX_

◆ dimY_