concepts::CircleMappingEdge2d Class Reference

#include <elementMaps.hh>

Inheritance diagram for concepts::CircleMappingEdge2d:

Public Member Functions
	CircleMappingEdge2d (const Real r, const Real2d vtx0, const Real2d vtx1)
	CircleMappingEdge2d (const Real2d center, const Real r, const Real angle0, const Real angle1)
	CircleMappingEdge2d (const Real2d vtx0, const Real2d vtxm, const Real2d vtx1)
	CircleMappingEdge2d (const CircleMappingEdge2d &edgemap)
	Copy Constructor.
virtual CircleMappingEdge2d *	clone () const
	Virtual copy constructor.
virtual MappingEdge2d *	inverse () const
	Returns the mapping of the edge in inverse direction.
bool	straight () const
	returns true if the mapping is straight, i.e. the radius equals zero.
virtual Real2d	operator() (const Real t) const
virtual Real2d	derivative (const Real t, const uint n=1) const
	Returns the n-th derivative.
virtual Real	curvature (const Real t, const uint n=0) const
MappingEdge2d *	part (const Real t0, const Real t1) const
virtual Real2d	normal (const Real t) const
	Returns the right normal vector, length is that of the derivative.
Real2d	n0 (const Real t) const
	Returns the normalised right normal vector.
const Real2d &	vtx (uint i) const
	Spit out one vertex of the edge.

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Protected Attributes
Real2d	vtx_ [2]
	Coordinates of the vertices at either end of the edge.

Detailed Description

2D element map for an circular arc.

The edge is given by two vertices and a radius that determines the curvature of the edge.

This class may be used in connection with BlendingQuad2d.

See also

BlendingQuad2d

Author

, Kersten Schmidt, 2004

Definition at line 259 of file elementMaps.hh.

Constructor & Destructor Documentation

CircleMappingEdge2d() [1/3]

concepts::CircleMappingEdge2d::CircleMappingEdge2d	(	const Real	r,
		const Real2d	vtx0,
		const Real2d	vtx1
	)

Constructor

Use the sign of the radius to bend the edge. r > 0 Arc is on the right side of line from 1st to 2nd vertex r < 0 Arc is on the left side of line from 1st to 2nd vertex

Minimal radius is half of the distance between the vertices.

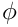
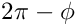
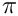
There are always two possibilites for the angle of the arc ( and . The smaller angle is taken. So the maximal angle is .

Parameters

r	radius
vtx0,vtx1	coordinates of the vertices

CircleMappingEdge2d() [2/3]

concepts::CircleMappingEdge2d::CircleMappingEdge2d	(	const Real2d	center,
		const Real	r,
		const Real	angle0,
		const Real	angle1
	)

Constructor

Parameters

center	center of the circle
r	radius
angle0	beginning angle
angle1	ending angle

CircleMappingEdge2d() [3/3]

concepts::CircleMappingEdge2d::CircleMappingEdge2d	(	const Real2d	vtx0,
		const Real2d	vtxm,
		const Real2d	vtx1
	)

Constructor

Use three points from the edge to find the radius and center. The basic formulae come from the following website, and then the full formulae derived by Mengyu Wang, 2011 http://mathforum.org/dr.math/faq/formulas/faq.analygeom_2.html#twocircles

Parameters

vtx0	beginning point
vtxm	middle point
vtx1	ending point

Member Function Documentation

clone()

virtual CircleMappingEdge2d * concepts::CircleMappingEdge2d::clone ( ) const

virtual

Virtual copy constructor.

Implements concepts::MappingEdge2d.

curvature()

virtual Real concepts::CircleMappingEdge2d::curvature ( const Real  t, const uint  n = 0  ) const

virtual

Returns the n-th derivative of the curvature.

It's implemented in general for n = 0,1 and works with curved edges. Can be overwritten in derived classes for performance reasons.

Reimplemented from concepts::MappingEdge2d.

derivative()

virtual Real2d concepts::CircleMappingEdge2d::derivative ( const Real  t, const uint  n = 1  ) const

virtual

Returns the n-th derivative.

Implements concepts::MappingEdge2d.

info()

virtual std::ostream & concepts::CircleMappingEdge2d::info ( std::ostream &  os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::MappingEdge2d.

inverse()

virtual MappingEdge2d * concepts::CircleMappingEdge2d::inverse ( ) const

virtual

Returns the mapping of the edge in inverse direction.

Reimplemented from concepts::MappingEdge2d.

n0()

Real2d concepts::MappingEdge2d::n0 ( const Real  t ) const

inlineinherited

Returns the normalised right normal vector.

Definition at line 107 of file elementMaps.hh.

operator()()

virtual Real2d concepts::CircleMappingEdge2d::operator() ( const Real  t ) const

virtual

Application operator. Maps the point from the parameter domain onto the physical space.

Implements concepts::MappingEdge2d.

part()

MappingEdge2d * concepts::CircleMappingEdge2d::part ( const Real  t0, const Real  t1  ) const

virtual

Returns a new object of an element map for a rectangular part of the reference cell defined by the two points.

Reimplemented from concepts::MappingEdge2d.

vtx()

const Real2d & concepts::MappingEdge2d::vtx ( uint  i ) const

inlineinherited

Spit out one vertex of the edge.

Definition at line 124 of file elementMaps.hh.

Member Data Documentation

vtx_

Real2d concepts::MappingEdge2d::vtx_[2]

protectedinherited

Coordinates of the vertices at either end of the edge.

Definition at line 128 of file elementMaps.hh.

---

The documentation for this class was generated from the following file:

• geometry/elementMaps.hh