Class documentation of Concepts
#include <elementMaps.hh>

Public Member Functions | |
| BlendingQuad2d (const MappingEdge2d *edgemap0, const MappingEdge2d *edgemap1, const MappingEdge2d *edgemap2, const MappingEdge2d *edgemap3=0, const Real2d *vtx0=0, const Real2d *vtx1=0, const Real2d *vtx2=0, const Real2d *vtx3=0) | |
| BlendingQuad2d (const BlendingQuad2d &v) | |
| Copy constructor. | |
| virtual Real2d | operator() (Real x, Real y) const |
| virtual MapReal2d | jacobian (const Real x, const Real y) const |
| Returns the Jacobian in a 2D linear map. | |
| virtual MapReal2d | hessian (uint i, const Real x, const Real y) const |
| virtual Real | lineElement (const Real x, const uint edge) const |
| virtual MappingEdge2d * | edge (const uint edge) const |
| virtual BlendingQuad2d * | clone () const |
| Returns a copy of the map. | |
| virtual Real | jacobianDeterminant (const Real x, const Real y) const |
| Returns determinant of the Jacobian. | |
| virtual MapReal2d | jacobianInverse (const Real x, const Real y) const |
| Returns the inverse of the Jacobian in a 2D linear map. | |
| virtual MapReal2d | inverseLaplace (const Real x, const Real y) const |
| virtual MappingQuad2d * | part (const Real2d x0, const Real2d y0) const |
| virtual bool | straight () const |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. | |
Detailed Description
A 2D element map for a curved quadrilateral.
The mapping is defined by the Linear Blending Function Method (proposed by Gordon and Hall, 1971). Therefor the mapping of the edges has to be given.
- Test:
- test::TestBlending2D
Definition at line 872 of file elementMaps.hh.
Constructor & Destructor Documentation
◆ BlendingQuad2d()
| concepts::BlendingQuad2d::BlendingQuad2d | ( | const MappingEdge2d * | edgemap0, |
| const MappingEdge2d * | edgemap1, | ||
| const MappingEdge2d * | edgemap2, | ||
| const MappingEdge2d * | edgemap3 = 0, |
||
| const Real2d * | vtx0 = 0, |
||
| const Real2d * | vtx1 = 0, |
||
| const Real2d * | vtx2 = 0, |
||
| const Real2d * | vtx3 = 0 |
||
| ) |
Constructor
Pointers to edge mappings and vertex coordinates can be given. There has to be given at least
- two opposite edges
- two adjacent edges and a the other vertex
- an edge and the two other vertices
- four vertices
If more edges or vertices are given, the particular coordinates of the vertices has to match.
The edges or vertices have to be given counter clockwise. The first vertex of the edgemap0 is the first vertex of the quad, the second in the edge map the second ...
The direction of an edge has to be changed by its method inverse(), e.g.
std::unique_ptr<MappingEdge2d> invEdge = edge.inverse(); BlendingQuad2d quad(invEdge, ...);
The class holds own copies of the given edge mappings and coordinates of the vertices.
First edge is 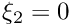
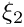
Member Function Documentation
◆ clone()
|
inlinevirtual |
Returns a copy of the map.
Implements concepts::MappingQuad2d.
Definition at line 920 of file elementMaps.hh.
◆ edge()
|
inlinevirtual |
Returns a copy of the edge mapping of one edge. The edge mappings are directed counter-clockwise, i.e. for the lower edge from the left lower vertex to the right lower one.
- Parameters
-
edge number of edge, i.e. 0 - lower, 1 - right, 2 - upper, 3 - left
Reimplemented from concepts::MappingQuad2d.
Definition at line 916 of file elementMaps.hh.
◆ hessian()
|
virtual |
Returns the Hessian in a 2D linear map
- Parameters
-
i coordinate (0 = x, 1 = y)
Implements concepts::MappingQuad2d.
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Reimplemented from concepts::MappingQuad2d.
◆ inverseLaplace()
◆ jacobian()
Returns the Jacobian in a 2D linear map.
Implements concepts::MappingQuad2d.
◆ lineElement()
Returns factor of differential element integrating over an edge.
The factor is either 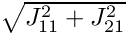
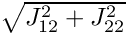
The routine exists explicitly because it is more efficient to implement it than to use jacobian itself, i.e. for affine elements the line element is constant.
- Parameters
-
x local variable on edge (in [0,1]), stands for 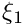
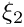
edge number of edge, i.e. 0: 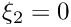
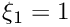
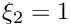
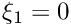
Reimplemented from concepts::MappingQuad2d.
◆ operator()()
Returns a point in 2D mapped from the unit square [0,1]2 onto the element in the original mesh.
- Returns
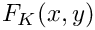
Implements concepts::MappingQuad2d.
◆ part()
|
virtualinherited |
Returns a new object of an element map for a rectangular part of the reference cell defined by the two points.
Reimplemented in concepts::VertexQuad2d.
◆ straight()
Reimplemented in concepts::VertexTriangle2d.
Definition at line 37 of file elementMaps.hh.
The documentation for this class was generated from the following file:
- geometry/elementMaps.hh
Generated on Wed Sep 13 2023 21:06:31 for Concepts by