concepts::KarniadakisNew< type, mode > Class Template Reference

Inheritance diagram for concepts::KarniadakisNew< type, mode >:

Public Member Functions
	KarniadakisNew (const int P, const QuadratureRule1d &quadrature, const int Q=0, const int R=0)
	KarniadakisNew (const int P, const Array< Real > &abscissas, const int Q=0, const int R=0)
	KarniadakisNew (const KarniadakisNew< type, mode > &Other)
	~KarniadakisNew ()
	Destructor.
uint	n () const
	Returns the number of shape functions.
uint	nP () const
const Real *	values () const
	Returns the values of the shape functions.

Protected Member Functions
void	init (const int P, const Real *xPoints, const int NxP, const int Q, const int R)
virtual std::ostream &	info (std::ostream &os) const=0
	Returns information in an output stream.

Protected Attributes
Real *	values_
	Values of the shape functions.

Detailed Description

template<int type, int mode>
class concepts::KarniadakisNew< type, mode >

Definition at line 22 of file karniadakisnew.hh.

Constructor & Destructor Documentation

KarniadakisNew() [1/3]

template<int type, int mode>

concepts::KarniadakisNew< type, mode >::KarniadakisNew	(	const int	P,
		const QuadratureRule1d &	quadrature,
		const int	Q = 0,
		const int	R = 0
	)

Constructor. Computes the values of the principal function of the given order and in the given points.

Parameters

P	Order of the principal function in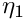
quadrature	Quadrature
Q	Order of the principal function in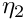
R	Order of the principal function in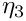
cache	Controls if the computed values should be taken from and stored in the cache

KarniadakisNew() [2/3]

template<int type, int mode>

concepts::KarniadakisNew< type, mode >::KarniadakisNew	(	const int	P,
		const Array< Real > &	abscissas,
		const int	Q = 0,
		const int	R = 0
	)

Constructor. Computes the values of the principal function of the given order and in the given points.

Parameters

P	Order of the principal function in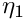
abscissas	array of points
Q	Order of the principal function in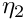
R	Order of the principal function in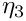
cache	Controls if the computed values should be taken from and stored in the cache

KarniadakisNew() [3/3]

template<int type, int mode>

concepts::KarniadakisNew< type, mode >::KarniadakisNew

(

const KarniadakisNew< type, mode > &

Other

)

Copy constructor

Parameters

Other

Element to be copied

Member Function Documentation

info()

virtual std::ostream & concepts::ShapeFunction1D< Real >::info ( std::ostream &  os ) const

protectedpure virtualinherited

Returns information in an output stream.

Reimplemented from concepts::OutputOperator.

Implemented in hp2D::NTElement_BA< F >::ShapeFunction, hp2D::NeumannTraceElement< F >::NTShapeFunction, hp2D::KarniadakisDeriv2, concepts::Karniadakis< type, mode >, concepts::Karniadakis< 1, 1 >, concepts::Laguerre, concepts::LaguerreBasis< mode >, concepts::Legendre, and concepts::Rys.

init()

template<int type, int mode>

void concepts::KarniadakisNew< type, mode >::init ( const int  P, const Real *  xPoints, const int  NxP, const int  Q, const int  R  )

protected

Computes the values of the principal function of the given order and in the given points.

(P+1)*(Q+1)*(R+1) is the number of shape functions which have to be computed in NxP points.

Parameters

P	Order of the principal function in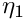
xPoints	Points
NxP	Number of points
Q	Order of the principal function in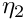
R	Order of the principal function in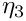

n()

uint concepts::ShapeFunction1D< Real >::n ( ) const

inlineinherited

Returns the number of shape functions.

Definition at line 35 of file shapefunction.hh.

nP()

uint concepts::ShapeFunction1D< Real >::nP ( ) const

inlineinherited

Returns the number of abscissas (in which the shape functions are evaluated)

Definition at line 38 of file shapefunction.hh.

values()

const Real * concepts::ShapeFunction1D< Real >::values ( ) const

inlineinherited

Returns the values of the shape functions.

Definition at line 40 of file shapefunction.hh.

Member Data Documentation

values_

Real * concepts::ShapeFunction1D< Real >::values_

protectedinherited

Values of the shape functions.

Definition at line 45 of file shapefunction.hh.

---

The documentation for this class was generated from the following file:

• integration/karniadakisnew.hh