 |
|
Class documentation of Concepts
#include <elementMaps3D.hh>
Public Member Functions | |
| PartMappingHexahedron3d (const MappingHexahedron3d &map, const Real3d x0, const Real3d x1) | |
| PartMappingHexahedron3d (const PartMappingHexahedron3d &other) | |
| PartMappingHexahedron3d * | clone () const override |
| Returns a copy of the map. | |
| Real3d | operator() (Real x, Real y, Real z) const override |
| MapReal3d | jacobian (const Real x, const Real y, const Real z) const override |
| MapReal3d | hessian (uint i, const Real x, const Real y, const Real z) const override |
| MappingQuad3d * | face (const uint face) const override |
| PartMappingHexahedron3d * | part (const Real3d x0, const Real3d x1) const override |
| virtual MapReal3d | jacobianInverse (const Real x, const Real y, const Real z) const |
| virtual Real | jacobianDeterminant (const Real x, const Real y, const Real z) const |
| Returns the determinant of the Jacobian. | |
Protected Member Functions | |
| std::ostream & | info (std::ostream &os) const override |
| Returns information in an output stream. | |
Detailed Description
A 3D element map for a restriction of a given hexahedron element mapping. Let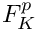 
![\[ F_K(s,t,u) = F^p_K(x_{0,0} (1-s) + x_{1,0} s,
x_{0,1} (1-t) + x_{1,1} t,
x_{0,2} (1-u) + x_{1,2} u). \]](form_388_dark.png)
- Todo:
- Possibly avoid copying the parent element (switch from unique_ptr to shared_ptr internally)
Definition at line 313 of file elementMaps3D.hh.
Constructor & Destructor Documentation
◆ PartMappingHexahedron3d()
| concepts::PartMappingHexahedron3d::PartMappingHexahedron3d | ( | const MappingHexahedron3d & | map, |
| const Real3d | x0, | ||
| const Real3d | x1 | ||
| ) |
Constructor
- Parameters
-
map Parent hexahedron element map x0,x1 lower left front and upper right back corner of the restricted domain in coordinates of the parent hexahedron
◆ ~PartMappingHexahedron3d()
|
inlineoverride |
Definition at line 323 of file elementMaps3D.hh.
Member Function Documentation
◆ clone()
|
overridevirtual |
Returns a copy of the map.
Implements concepts::MappingHexahedron3d.
◆ face()
|
overridevirtual |
Returns the mapping of the given face.
Implements concepts::MappingHexahedron3d.
◆ hessian()
|
overridevirtual |
Returns the Hessian, the integer indicates which 3x3 submap of the 3x3xi (i=1..3) tensor is required
Implements concepts::MappingHexahedron3d.
◆ info()
|
overrideprotectedvirtual |
Returns information in an output stream.
Implements concepts::MappingHexahedron3d.
◆ jacobian()
![\[ \left(\frac{\partial F_K}{\partial\vec\xi}\right) =
\left\{\frac{\partial x^i}{\partial \xi_j}\right\}_{i,j=1}^3 \]](form_396_dark.png)
◆ jacobianDeterminant()
|
inlinevirtualinherited |
Returns the determinant of the Jacobian.
Reimplemented in concepts::MapHexahedron3d.
Definition at line 200 of file elementMaps3D.hh.
◆ jacobianInverse()
|
inlinevirtualinherited |
Computes the inverse of the jacobian:
![\[ \left(\frac{\partial F_K}{\partial\vec\xi}\right)^{-1} =
\left\{\frac{\partial \xi_i}{\partial x^j}\right\}_{i,j=1}^3 \]](form_397_dark.png)
Reimplemented in concepts::MapHexahedron3d.
Definition at line 196 of file elementMaps3D.hh.
◆ operator()()
|
overridevirtual |
Returns a point in 3D mapped from the unit cube [0,1]3 onto the element in physical 3d space.
- Returns
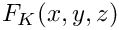
Implements concepts::MappingHexahedron3d.
◆ part()
|
overridevirtual |
Returns a part of the mapping
Implements concepts::MappingHexahedron3d.
The documentation for this class was generated from the following file:
- geometry/elementMaps3D.hh
Generated on Wed Sep 13 2023 21:06:42 for Concepts by
1.9.8