#include <quadRule.hh>

Inheritance diagram for concepts::QuadratureRule2dQuadDuffy:

Public Member Functions
	QuadratureRule2dQuadDuffy (Real beta, uint nx, uint ny, uint noVtx=0)

virtual const Real *	weights (uint i=0) const

const uint	n (uint i=0) const

virtual bool	quadratureData (const uint i, Real3d &q, Real &w) const

virtual const bool	domain () const

virtual const bool	tensor () const

void	printData () const

virtual const Real *	abscissas (uint i) const

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Protected Attributes
const Real *	intX_
	Abscissas.

const Real *	intY_

Detailed Description

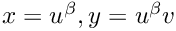
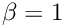
Class representing the Generalized Duffy quadrature rule in 2d, $x = u^\beta, y = u^\beta v$ , that is for $\beta=1$ the standard duffy integration rule.

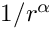
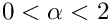
The quadrature rule is not tensored and is most effective to integrate $1/r^\alpha$ singularities, for $0<\alpha < 2$ .

The weights are given in .

This class is motivated by the paper "Generalized Duffy Transformation for Integrating Vertex Singularites" by Mousavi / Sukumar

The quadrature rule depends on the duffy parameter beta. beta should be chosen such that

$2\beta -1 -\alpha\beta \geq 0$

.

Note that for too big beta, the quadrature points in become very close to the origin. This should be taken into account, regarding mashine precision. Due to this fact the singular local vertex by default is in origin.

The abscissas are computed on .

The internal compute routine computes generalized duffy points on a triangle. With that, the method can be used for arbitrary reference geometries that can be subdivided into triangles with common singularity vertex.

The quadrature points on the transformed triangles are computed with underlying Gauss-Legrendre points, whose number can be chosen individual in each direction in the transformed quad.

Author: Robert Gruhlke, 2014

Definition at line 481 of file quadRule.hh.

Constructor & Destructor Documentation

◆ QuadratureRule2dQuadDuffy()

concepts::QuadratureRule2dQuadDuffy::QuadratureRule2dQuadDuffy	(	Real	beta,
		uint	nx,
		uint	ny,
		uint	noVtx = `0`
	)

Constructor

The singular vertex is by default set to zero. This is ok, since when building the mesh one can place the geometry s.t. the first elements vertex lies on the singularity.

Parameters

beta	generalized duffy transformation parameter
nx	number of quadrature points of underlying Gauss-Legendre points in x-direction on transformed square.
ny	number of quadrature points of underlying Gauss-Legendre points in y-direction on transformed square.
noVtx	number of local vertex