Class documentation of Concepts
#include <smatrix.hh>

Public Member Functions | |
| virtual void | operator() (const TColumn< F > &src, TColumn< F > &dest) const =0 |
| Application operator. | |
| virtual uint | size () const =0 |
| Returns the size of the S matrix. | |
Protected Member Functions | |
| virtual std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. | |
Detailed Description
class concepts::SMatrixBase< F >
An abstract class for an S matrix.
An S matrix describes how a T matrix has to be changed to reflect a refinement of an element.
The definition of an S matrix is as follows:
Let 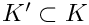
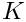
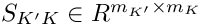
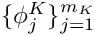
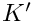
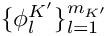
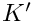
![\[
\phi_j^K|_{K'} = \sum_{l=1}^{m_{K'}} [S_{K'K}]_{lj} \phi_l^{K'}
\]](form_755.png)
and in vector notation: 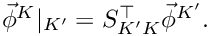
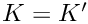
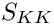
- See also
- TMatrixBase
- TColumn
Definition at line 55 of file smatrix.hh.
Member Function Documentation
◆ info()
|
protectedvirtual |
Returns information in an output stream.
Reimplemented from concepts::OutputOperator.
Reimplemented in concepts::SMatrix1D, concepts::SMatrixTensor< F, dim >, concepts::SMatrixCompose< F >, concepts::SMatrixGeneralTensor< F, dim >, and concepts::SMatrixBlock< F, dim >.
◆ operator()()
|
pure virtual |
Application operator.
Implemented in concepts::SMatrixTensor< F, dim >, concepts::SMatrixCompose< F >, concepts::SMatrixGeneralTensor< F, dim >, concepts::SMatrixBlock< F, dim >, and concepts::SMatrix1D.
◆ size()
|
pure virtual |
Returns the size of the S matrix.
Implemented in concepts::SMatrix1D, concepts::SMatrixTensor< F, dim >, concepts::SMatrixCompose< F >, concepts::SMatrixGeneralTensor< F, dim >, and concepts::SMatrixBlock< F, dim >.
The documentation for this class was generated from the following files:
- hp2D/hpAdaptiveSpaceH1.hh
- space/smatrix.hh
Generated on Wed Sep 13 2023 21:06:45 for Concepts by
