You are here: Concepts>Concepts Web>Class documentation

Class documentation of Concepts

Loading...
Searching...
No Matches
Public Types | Public Member Functions | Protected Member Functions | List of all members
eigensolver::ArPack< F, G, H > Class Template Reference

#include <ARPACK.hh>

Inheritance diagram for eigensolver::ArPack< F, G, H >:
eigensolver::EigenSolver< F > concepts::OutputOperator

Public Types

enum  which {
  LM , SM , LR , SR ,
  LI , SI
}
 
enum  modus { NORMAL = 1 , REGINV = 2 , SHIFTINV = 3 , SHIFTINVIMAG = 4 }
 

Public Member Functions

 ArPack (concepts::Operator< G > &OP, concepts::Operator< F > &A, concepts::Operator< H > &B, const int kmax=1, const Real tol=0.0, const int maxiter=300, enum which target=SM, enum modus mode=REGINV, const F sigma=0.0, const concepts::Vector< F > *start=0, const concepts::Array< F > *resid=0, const bool schur=false)
 
virtual const concepts::Array< F > & getEV ()
 
virtual const concepts::Array< concepts::Vector< F > * > & getEF ()
 
virtual uint iterations () const
 Returns the number of iterations.
 
virtual uint converged () const
 Returns the number of converged eigenpairs.
 
concepts::Array< F > getRESID ()
 Returns the RESID vector:
 

Protected Member Functions

virtual std::ostream & info (std::ostream &os) const
 Returns information in an output stream.
 

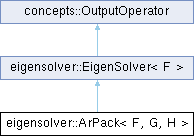
Detailed Description

template<typename F, typename G = Real, typename H = Real>
class eigensolver::ArPack< F, G, H >

Eigenvalue solver using ARPACK, the routine dnaupd or znaupd.

ARPACK is designed to solve large scale eigenvalue problems. The package is designed to compute a few eigenvalues and corresponding eigenvectors of a general n by n matrix A. It is most appropriate for large sparse or structured matrices A. This software is based upon an algorithmic variant of the Arnoldi process called the Implicitly Restarted Arnoldi Method (IRAM). When the matrix A is symmetric it reduces to a variant of the Lanczos process called the Implicitly Restarted Lanczos Method (IRLM). These variants may be viewed as a synthesis of the Arnoldi/Lanczos process with the Implicitly Shifted QR technique that is suitable for large scale problems.

ARPACK software is capable of solving large scale symmetric, nonsymmetric, and generalized eigenproblems from significant application areas. The software is designed to compute a few (k) eigenvalues with user specified features such as those of largest real part or largest magnitude. No auxiliary storage is required. A set of Schur basis vectors for the desired k-dimensional eigen-space is computed which is numerically orthogonal to working precision. Numerically accurate eigenvectors are available on request.

dnaupd uses implicitly restarted Arnoldi iteration to solve the generalized eigenvalue problem 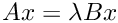$ A x = \lambda B x $ with A general non-symmetric and B symmetric and positive definite. For A symmetric, use ArPackSymm instead.

znaupd uses implicitly restarted Arnoldi iteration to solve the generalized eigenvalue problem 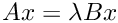$ A x = \lambda B x $ with A general non-symmetric, complex and B symmetric and positive definite, real. For A symmetric and complex also use this routine.

See also
Richard B. Lehoucq, Kristyn J. Maschhoff, Danny C. Sorensen, and Chao Yang, ARPACK Homepage.
Richard B. Lehoucq, Danny C. Sorensen, and Chao Yang. ARPACK users' guide. Software, Environments, and Tools. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1998.
Author
Christoph Winkelmann, 2004

Definition at line 70 of file ARPACK.hh.

Member Enumeration Documentation

◆ modus

template<typename F , typename G = Real, typename H = Real>
enum eigensolver::ArPack::modus

Specify mode of ARPACK which should be used to compute the Ritz values $ \nu $ of OP.

Definition at line 92 of file ARPACK.hh.

◆ which

template<typename F , typename G = Real, typename H = Real>
enum eigensolver::ArPack::which

Specify which of the Ritz values $ \nu $ of OP (described in modus) to compute.

Definition at line 75 of file ARPACK.hh.

Constructor & Destructor Documentation

◆ ArPack()

template<typename F , typename G = Real, typename H = Real>
eigensolver::ArPack< F, G, H >::ArPack ( concepts::Operator< G > &  OP,
concepts::Operator< F > &  A,
concepts::Operator< H > &  B,
const int  kmax = 1,
const Real  tol = 0.0,
const int  maxiter = 300,
enum which  target = SM,
enum modus  mode = REGINV,
const F  sigma = 0.0,
const concepts::Vector< F > *  start = 0,
const concepts::Array< F > *  resid = 0,
const bool  schur = false 
)

Constructor.

Parameters
OPOperator OP as described in modus
AStiffness matrix
BOperator B as descirbed in modus
kmaxNumber of eigenpairs to be computed
tolConvergence tolerance for the eigenpairs. The default value 0.0 is replaced by DLAMCH('EPS') from LAPACK.
maxiterMaximum number of Arnoldi iterations allowed
targetWhat sort of eigenvalues to compute
modeMode in which ARPACK should be used
sigmaShift for the shift-invert modes
startInitial vector for iteration
schurCalculate Schur vector basis instead of eigenvectors

Member Function Documentation

◆ converged()

template<typename F , typename G = Real, typename H = Real>
virtual uint eigensolver::ArPack< F, G, H >::converged ( ) const
inlinevirtual

Returns the number of converged eigenpairs.

Implements eigensolver::EigenSolver< F >.

Definition at line 150 of file ARPACK.hh.

◆ getEF()

template<typename F , typename G = Real, typename H = Real>
virtual const concepts::Array< concepts::Vector< F > * > & eigensolver::ArPack< F, G, H >::getEF ( )
virtual

Returns an array with the eigenfunctions. If eigenvalue k is real, entry k contains the (real) eigenfunction. If eigenvalues k and k+1 are complex conjugate, entry k contains the real part of and entry k+1 contains the imaginary part of eigenfunction k. Eigenfunction k+1 is the complex conjugate of eigenfunction k.

Implements eigensolver::EigenSolver< F >.

◆ getEV()

template<typename F , typename G = Real, typename H = Real>
virtual const concepts::Array< F > & eigensolver::ArPack< F, G, H >::getEV ( )
virtual

Returns an array with the real parts of the eigenvalues in the first kmax entries and the imaginary parts of the eigenvalues in the second kmax entries.

Implements eigensolver::EigenSolver< F >.

◆ getRESID()

template<typename F , typename G = Real, typename H = Real>
concepts::Array< F > eigensolver::ArPack< F, G, H >::getRESID ( )
inline

Returns the RESID vector:

Definition at line 152 of file ARPACK.hh.

◆ info()

template<typename F , typename G = Real, typename H = Real>
virtual std::ostream & eigensolver::ArPack< F, G, H >::info ( std::ostream &  os) const
protectedvirtual

Returns information in an output stream.

Reimplemented from eigensolver::EigenSolver< F >.

◆ iterations()

template<typename F , typename G = Real, typename H = Real>
virtual uint eigensolver::ArPack< F, G, H >::iterations ( ) const
inlinevirtual

Returns the number of iterations.

Implements eigensolver::EigenSolver< F >.

Definition at line 148 of file ARPACK.hh.

The documentation for this class was generated from the following file:
Generated on Wed Sep 13 2023 21:06:49 for Concepts by doxygen 1.9.8