eigensolver::ArPackSymm Class Reference

#include <ARPACKsymm.hh>

Inheritance diagram for eigensolver::ArPackSymm:

Public Types
enum	which {   LA , SA , LM , SM ,   BE }
enum	modus {   NORMAL = 1 , REGINV = 2 , SHIFTINV = 3 , BUCKLING = 4 ,   CAYLEY = 5 }

Public Member Functions
	ArPackSymm (concepts::Operator< Real > &OP, concepts::Operator< Real > &A, concepts::Operator< Real > &B, const int kmax=1, const Real tol=0.0, const int maxiter=300, enum which target=SM, enum modus mode=REGINV, const Real sigma=0.0, const concepts::Vector< Real > *start=0)
virtual const concepts::Array< Real > &	getEV ()
virtual const concepts::Array< concepts::Vector< Real > * > &	getEF ()
virtual uint	iterations () const
	Returns the number of iterations.
virtual uint	converged () const
	Returns the number of converged eigen pairs.

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

Eigenvalue solver using ArPack, the routine dsaupd.

ArPack is designed to solve large scale eigenvalue problems. The package is designed to compute a few eigenvalues and corresponding eigenvectors of a general n by n matrix A. It is most appropriate for large sparse or structured matrices A. This software is based upon an algorithmic variant of the Arnoldi process called the Implicitly Restarted Arnoldi Method (IRAM). When the matrix A is symmetric it reduces to a variant of the Lanczos process called the Implicitly Restarted Lanczos Method (IRLM). These variants may be viewed as a synthesis of the Arnoldi/Lanczos process with the Implicitly Shifted QR technique that is suitable for large scale problems.

ArPack software is capable of solving large scale symmetric, nonsymmetric, and generalized eigenproblems from significant application areas. The software is designed to compute a few (k) eigenvalues with user specified features such as those of largest real part or largest magnitude. No auxiliary storage is required. A set of Schur basis vectors for the desired k-dimensional eigen-space is computed which is numerically orthogonal to working precision. Numerically accurate eigenvectors are available on request.

dsaupd uses implicitly restarted Arnoldi iteration to solve the generalized eigenvalue problem with B symmetric and positive definite. For symmetric problems this reduces to a variant of the Lanczos method.

See also

Richard B. Lehoucq, Kristyn J. Maschhoff, Danny C. Sorensen, and Chao Yang, ArPackSymm Homepage.

Richard B. Lehoucq, Danny C. Sorensen, and Chao Yang. ArPackSymm users' guide. Software, Environments, and Tools. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 1998.

Test:

test::GolubExample

test::GolubExampleSum

test::MaxwellTransmissionEVP

Author

Philipp Frauenfelder, 2002

Definition at line 65 of file ARPACKsymm.hh.

Member Enumeration Documentation

modus

enum eigensolver::ArPackSymm::modus

Specify mode of ArPackSymm which should be used to compute the Ritz values 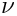of OP.

Definition at line 87 of file ARPACKsymm.hh.

which

enum eigensolver::ArPackSymm::which

Specify which of the Ritz values 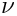of OP (described in modus) to compute.

Definition at line 70 of file ARPACKsymm.hh.

Constructor & Destructor Documentation

ArPackSymm()

eigensolver::ArPackSymm::ArPackSymm	(	concepts::Operator< Real > &	OP,
		concepts::Operator< Real > &	A,
		concepts::Operator< Real > &	B,
		const int	kmax = 1,
		const Real	tol = 0.0,
		const int	maxiter = 300,
		enum which	target = SM,
		enum modus	mode = REGINV,
		const Real	sigma = 0.0,
		const concepts::Vector< Real > *	start = 0
	)

Constructor.

Parameters

OP	Operator OP as described in modus
A	Stiffness matrix
B	Operator B as descirbed in modus
kmax	Number of eigenpairs to be computed
tol	Convergence tolerance for the eigenpairs. The default value 0.0 is replaced by DLAMCH('EPS') from LAPACK.
maxiter	Maximum number of Arnoldi iterations allowed
target	What sort of eigenvalues to compute
mode	Mode in which ArPackSymm should be used
sigma	Shift for the shift-invert, Buckling or Cayley mode

Member Function Documentation

converged()

virtual uint eigensolver::ArPackSymm::converged ( ) const

inlinevirtual

Returns the number of converged eigen pairs.

Implements eigensolver::EigenSolver< Real >.

Definition at line 133 of file ARPACKsymm.hh.

getEF()

virtual const concepts::Array< concepts::Vector< Real > * > & eigensolver::ArPackSymm::getEF ( )

virtual

Implements eigensolver::EigenSolver< Real >.

getEV()

virtual const concepts::Array< Real > & eigensolver::ArPackSymm::getEV ( )

virtual

Returns an array with the eigen values

Deprecated:

: this interface requires that the returned array must be hold as a member variable of the class. (use std::auto_pointer or similar)

Implements eigensolver::EigenSolver< Real >.

info()

virtual std::ostream & eigensolver::ArPackSymm::info ( std::ostream &  os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from eigensolver::EigenSolver< Real >.

iterations()

virtual uint eigensolver::ArPackSymm::iterations ( ) const

inlinevirtual

Returns the number of iterations.

Implements eigensolver::EigenSolver< Real >.

Definition at line 132 of file ARPACKsymm.hh.

---

The documentation for this class was generated from the following file:

• eigensolver/ARPACKsymm.hh