#include <constrained.hh>

Inheritance diagram for eigensolver::Constrained:

Public Member Functions
	Constrained (concepts::Operator< Real > &A, concepts::Operator< Real > &M, const concepts::SparseMatrix< Real > &C, SolverFabric< Real > &solver)

virtual const concepts::Array< Real > &	getEV ()

virtual const concepts::Array< concepts::Vector< Real > * > &	getEF ()

virtual uint	iterations () const
	Returns the number of iterations.

virtual uint	converged () const
	Returns the number of converged eigen pairs.

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

Solves a generalized eigenvalue problem subject to linear, homogeneous constraints.

This class solve a generalized eigenvalue problem of the form

$A \vec x = \lambda M \vec x$

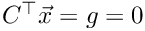
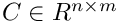
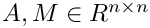
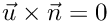
subject to the constraints $C^\top \vec x = g = 0$ where $C \in R^{n \times m}$ and $A, M \in R^{n \times n}$ . This is important for solving eigenvalue problems with essential boundary conditions like $\vec u \times \vec n = 0$ .

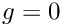
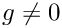
For the case , this is described in [1 section 12.6, 2]. For the much more complicated case of $g \neq 0$ , see [3, 4]. The first case should be sufficient for most applications.

See also: [1] Gene H. Golub and Charles F. van Loan, Matrix Computations, The Johns Hopkins University Press, 1983.
[2] Gene H. Golub, Some Modified Matrix Eigenvalue Problems, SIAM Review, 15 (1973), No. 2, 318–334.
[3] Walter Gander, Gene H. Golub and Urs von Matt, A Constrained Eigenvalue Problem, in Numerical Linear Algebra, Digital Signal Processing and Parallel Algorithms, Gene H. Golub and P. Van Dooren (eds.), NATO ASI Series, Vol. F70, 1991, 677–686.
[4] Walter Gander, Gene H. Golub and Urs von Matt, A Constrained Eigenvalue Problem, Linear Algebra and Its Applications, 114/115 (1989), 815–839.

Test:: test::ConstrainedEVP

Author: Philipp Frauenfelder, 2002

Definition at line 54 of file constrained.hh.

Constructor & Destructor Documentation

◆ Constrained()

eigensolver::Constrained::Constrained	(	concepts::Operator< Real > &	A,
		concepts::Operator< Real > &	M,
		const concepts::SparseMatrix< Real > &	C,
		SolverFabric< Real > &	solver
	)

inline

Constructor.

Parameters

A	Matrix
M	Matrix
C	Matrix of constraints
solver	Fabric for the eigenvalue solver

Definition at line 62 of file constrained.hh.

Member Function Documentation

◆ converged()

virtual uint eigensolver::Constrained::converged ( ) const

inlinevirtual

Returns the number of converged eigen pairs.

Implements eigensolver::EigenSolver< Real >.

Definition at line 74 of file constrained.hh.

◆ getEF()

virtual const concepts::Array< concepts::Vector< Real > * > & eigensolver::Constrained::getEF ( )

virtual

Implements eigensolver::EigenSolver< Real >.

◆ getEV()

virtual const concepts::Array< Real > & eigensolver::Constrained::getEV ( )

virtual

Returns an array with the eigen values

Deprecated:: : this interface requires that the returned array must be hold as a member variable of the class. (use std::auto_pointer or similar)

Implements eigensolver::EigenSolver< Real >.

◆ info()

virtual std::ostream & eigensolver::Constrained::info ( std::ostream & os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from eigensolver::EigenSolver< Real >.

◆ iterations()

virtual uint eigensolver::Constrained::iterations ( ) const

inlinevirtual

Returns the number of iterations.

Implements eigensolver::EigenSolver< Real >.

Definition at line 73 of file constrained.hh.

The documentation for this class was generated from the following file:

eigensolver/constrained.hh

Class documentation of Concepts

Public Member Functions

Protected Member Functions

Detailed Description

Constructor & Destructor Documentation

◆ Constrained()

Member Function Documentation

◆ converged()

◆ getEF()

◆ getEV()

◆ info()

◆ iterations()