#include <sparseMatrix.hh>

Inheritance diagram for concepts::SparseMatrix< F >:

Public Types
typedef Realtype< F >::type	r_type
	Real type of data type.

typedef Cmplxtype< F >::type	c_type
	Complex type of data type.

typedef std::conditional< std::is_same< typenameRealtype< F >::type, F >::value, typenameRealtype< F >::type, typenameCmplxtype< F >::type >::type	d_type
	Data type, depending if F is real or complex.

typedef _HashedSMatrix_iterator< F, F &, F * >	iterator

typedef _HashedSMatrix_iterator< F, const F &, const F * >	const_iterator

typedef F	value_type

typedef F	type
	Type of data, e.g. matrix entries.

Public Member Functions
template<class G >
	SparseMatrix (const Space< G > &spcX, const Space< G > &spcY)

	SparseMatrix (uint nofrows, uint nofcols)

	SparseMatrix (uint dim=0)

template<class G >
	SparseMatrix (const Space< G > &spcX, const Space< G > &spcY, const BilinearForm< F, G > &bf, const Real eps=0.0, const bool single=false)

template<class G >
	SparseMatrix (const Space< G > &spcX, const Space< G > &spcY, const Sequence< bool > &seq, const BilinearForm< F, G > &bf, const Real eps=0.0, const bool single=false)

template<class G >
	SparseMatrix (const Space< G > &spcX, const Space< G > &spcY, const BilinearForm< F, G > &bf, const Sequence< ElementWithCell< G > * > &seq, const Real eps=0.0)

template<class G >
	SparseMatrix (const Space< G > &spc, const BilinearForm< F, G > &bf, const Real eps=0.0)

	SparseMatrix (const Space< typename Realtype< F >::type > &spc, const BilinearFormContainer< F > bf, const Real eps=0.0)

template<class G >
	SparseMatrix (const Space< G > &spc, const Sequence< bool > &seq, const BilinearForm< F, G > &bf, const Real eps=0.0)

template<class G >
	SparseMatrix (const Space< G > &spc, const BilinearForm< F, G > &bf, const Sequence< ElementWithCell< G > * > &seq, const Real eps=0.0)

	SparseMatrix (const SparseMatrix< F > &m, bool t=false)

template<class G >
	SparseMatrix (const Space< G > &spc, const F *const v, const int i=-1)

template<class G >
	SparseMatrix (const Space< G > &spc, const Vector< F > &x, const Vector< F > &y)

template<class H >
	SparseMatrix (Operator< H > &A, bool slow=false)

void	operator= (const SparseMatrix< F > &)

template<class H >
	SparseMatrix (const SparseMatrix< H > &fncX, F fnc(const H &))

template<class H >
	SparseMatrix (const SparseMatrix< H > &fncX, const F &fnc(const H &))

template<class H >
	SparseMatrix (const SparseMatrix< H > &fncX)

virtual void	operator() (const Function< r_type > &fncY, Function< F > &fncX)

virtual void	operator() (const Function< c_type > &fncY, Function< c_type > &fncX)

template<class H , class I >
void	operator() (const Vector< H > &fncY, Vector< I > &fncX)
	Multiplies the matrix with `fncY`. The result is `fncX`.

const_iterator	begin (uint row=0) const

iterator	begin (uint row=0)

const_iterator	end () const
	Last entrance of the particular order.

virtual void	transpMult (const Vector< r_type > &fncY, Vector< F > &fncX)

virtual void	transpMult (const Vector< c_type > &fncY, Vector< c_type > &fncX)

virtual F	operator() (const uint i, const uint j) const
	Returns entry with indices `i` and `j`.

virtual F &	operator() (const uint i, const uint j)
	Returns and allows access to entry with indices `i` and `j`.

SparseMatrix< F > &	operator*= (const F factor)

virtual void	resize (uint m, uint n)
	Sets a new size, previous data might be lost

void	write (char *fname) const

bool	storeMatlab (const std::string filename, const std::string name="", bool append=false) const

const HashedSparseMatrix< F > *	m () const
	Returns the sparse matrix itself.

template<class H , class I >
void	addInto (Matrix< H > &dest, const I fact, const uint rowoffset=0, const uint coloffset=0) const

template<class H , class I >
void	addIntoT (Matrix< H > &dest, const I fact, const uint rowoffset=0, const uint coloffset=0) const

template<class H , class I >
void	add (const Vector< H > &v, const I fact, const uint rowoffset=0, const uint coloffset=0)

template<class H , class I >
void	addT (const Vector< H > &v, const I fact, const uint rowoffset=0, const uint coloffset=0)

void	multiply (const SparseMatrix< F > &fact, Matrix< F > &dest) const
	Multiplies this matrix with `fact` and adds the result to `dest`.

template<class H >
void	multiply (const H &fact, Matrix< F > &dest) const
	Multiplies this matrix with `fact` and adds the result to `dest`.

virtual uint	used () const
	Returns the number of used entries in the matrix.

float	memory () const
	Memory usage in byte.

void	symmetrize ()
	Makes sure a theoretically symmetric matrix is symmetric in memory too.

void	compress (Real threshold=EPS)

void	histogram (std::map< int, uint > &hist) const
	Creates a histogram of the matrix entries.

void	copy (const SparseMatrix< F > &n)
	Copies `n` to this matrix.

virtual void	convertCRS (F a, int asub, int *xa) const

virtual void	convertCCS (F a, int asub, int *xa) const

virtual void	convertIJK (F , int , int *) const

const uint	nofRows () const
	Number of rows.

const uint	nofCols () const
	Number of columns.

iterator	end ()
	Iterator, standing behind last element.

virtual void	set (const uint i, const uint j, const F value, const bool use_threshold=false, const Real threshold_value=1e-8)

virtual void	add (const uint i, const uint j, const F value, const bool use_threshold=false, const Real threshold_value=1e-8)

virtual void	operator() (const Function< r_type > &fncY, Function< F > &fncX)=0
	Computes `fncX` = A(`fncY`) where A is this matrix.

virtual void	operator() ()

virtual bool	operator== (const Matrix< F > &otherMat) const

virtual void	transpMult (const Vector< r_type > &fncY, Vector< F > &fncX)=0
	Computes `fncX` = A^T `fncY` where A is this matrix.

virtual const uint	dimX () const

virtual const uint	dimY () const

virtual void	show_messages ()

Static Public Member Functions
template<class G >
static void	assembly (Matrix< F > &dest, const Space< G > &spc, const BilinearForm< F, G > &bf, const Real threshold=0.0)

template<class G >
static void	assembly (Matrix< F > &dest, Scan< Element< G > > *sc, const BilinearForm< F, G > &bf, const Real threshold=0.0)

template<class G >
static void	assembly (Matrix< F > &dest, const Sequence< ElementWithCell< G > * > seq, const BilinearForm< F, G > &bf, const Real threshold=0.0)

template<class G >
static void	assembly (Matrix< F > &dest, const Space< G > &spc, const Sequence< bool > &seq, const BilinearForm< F, G > &bf, const Real threshold=0.0)

template<class G >
static void	assembly (Matrix< F > &dest, const Space< G > &spcX, const Space< G > &spcY, const BilinearForm< F, G > &bf, const Real threshold=0.0, const bool single=false)

template<class G >
static void	assembly (Matrix< F > &dest, const Sequence< ElementWithCell< G > * > seqX, const Space< G > &spcY, const BilinearForm< F, G > &bf, const Real threshold=0.0)

template<class G >
static void	assembly (Matrix< F > &dest, const BilinearForm< F, G > &bf, const ElementPairList< G > &pairs)

template<class G >
static void	assembly (Matrix< F > &dest, const Space< G > &spcX, const Space< G > &spcY, const Sequence< bool > &seq, const BilinearForm< F, G > &bf, const Real threshold=0.0, const bool single=false)

Timing Interface
These functions are used to get timings from class internal computations. The values are stored in a user defined concepts::InOutParameters structure in different arrays (see `setTimings`). These arrays can be grouped into a table for easier postprocessing with concepts::ResultsTable table; table.addMap(concepts::ResultsTable::DOUBLE, "jacobian", output); table.addMap(concepts::ResultsTable::DOUBLE, "whole_sumfact", output); std::ofstream ofs("table.gnuplot"); ofs << std::setprecision(20); table.print<concepts::ResultsTable::GNUPLOT>(ofs); concepts::ResultsTable Definition resultsTable.hh:23 concepts::makeSet Set< F > makeSet(uint n, const F &first,...) Definition set.hh:320
static void	setTimings (InOutParameters *timings)

static bool	timings ()

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Protected Attributes
uint	dimX_
	Dimension of image space and the source space.

uint	dimY_

Detailed Description

template<class F>
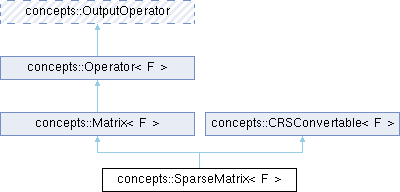
class concepts::SparseMatrix< F >

Sparse matrix. The matrix has the size m x n where m is the dimension of the image space (spaceX) and n is the dimension of the source space (spaceY).

The matrix is setup and assembled in the constructor. It calls the bilinear form on every element of the space and uses the T matrices of the elements to assemble the element matrices into the global matrix.

There are quite a few solver which can be used to solve the system.

See also: TMatrixBase; CG; GMRes

Test:

test::CompositionsTest

test::MoreCompositionsTest

test::DriverTest

test::SparseMatrixTest

Examples: BGT_0.cc, RobinBCs.cc, arpackppTutorial.cc, elasticity2D_tutorial.cc, exactDtN.cc, howToGetStarted.cc, hpFEM2d-simple.cc, hpFEM2d.cc, hpFEM3d-EV.cc, inhomDirichletBCs.cc, inhomDirichletBCsLagrange.cc, inhomNeumannBCs.cc, linearDG1d.cc, linearFEM1d-simple.cc, linearFEM1d.cc, matfileTutorial.cc, and parallelizationTutorial.cc.

Definition at line 65 of file sparseMatrix.hh.

Member Typedef Documentation

◆ c_type

template<class F >

typedef Cmplxtype<F>::type concepts::SparseMatrix< F >::c_type

Complex type of data type.

Definition at line 70 of file sparseMatrix.hh.

◆ const_iterator

template<class F >

typedef _HashedSMatrix_iterator<F, const F&, const F*> concepts::SparseMatrix< F >::const_iterator

Definition at line 76 of file sparseMatrix.hh.

◆ d_type

template<class F >

typedef std::conditional<std::is_same<typenameRealtype<F>::type,F>::value,typenameRealtype<F>::type,typenameCmplxtype<F>::type>::type concepts::SparseMatrix< F >::d_type

Data type, depending if F is real or complex.

Definition at line 73 of file sparseMatrix.hh.

◆ iterator

template<class F >

typedef _HashedSMatrix_iterator<F, F&, F*> concepts::SparseMatrix< F >::iterator

Definition at line 75 of file sparseMatrix.hh.

◆ r_type

template<class F >

typedef Realtype<F>::type concepts::SparseMatrix< F >::r_type

Real type of data type.

Definition at line 68 of file sparseMatrix.hh.

◆ type

template<class F >

typedef F concepts::Operator< F >::type

inherited

Type of data, e.g. matrix entries.

Definition at line 45 of file compositions.hh.

◆ value_type

template<class F >

typedef F concepts::Matrix< F >::value_type

inherited

Definition at line 41 of file matrix.hh.

Constructor & Destructor Documentation

◆ SparseMatrix() [1/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spcX,
		const Space< G > &	spcY
	)

inline

Constructor. Creates an empty matrix.

Definition at line 81 of file sparseMatrix.hh.

◆ SparseMatrix() [2/17]

template<class F >

concepts::SparseMatrix< F >::SparseMatrix	(	uint	nofrows,
		uint	nofcols
	)

inline

Constructor. Creates an empty matrix.

Definition at line 90 of file sparseMatrix.hh.

◆ SparseMatrix() [3/17]

template<class F >

concepts::SparseMatrix< F >::SparseMatrix ( uint dim = 0 )

inline

Definition at line 96 of file sparseMatrix.hh.

◆ SparseMatrix() [4/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spcX,
		const Space< G > &	spcY,
		const BilinearForm< F, G > &	bf,
		const Real	eps = `0.0`,
		const bool	single = `false`
	)

Constructor. Computes the global matrix by assembling the element matrices.

This constructor features a double loop over the elements of the image and the source space. On each combination, the bilinear form is called. You can force this constructor to execute the double loop in such a way that only for diagonal combinations of the elements in both space the integration and assembling is executed. Use single and set it to true.

Use this constructor, if spcX != spcY or if you have local matrices which express the interaction of the two elements., const Real eps = 0.0, const Real eps = 0.0

In non-symmetric FEM (eg. DGFEM), one has to solve A^T u = f. This constructor computes A and not A^T.

Parameters

spcX	Image space
spcY	Source space
bf	Bilinear form
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [5/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spcX,
		const Space< G > &	spcY,
		const Sequence< bool > &	seq,
		const BilinearForm< F, G > &	bf,
		const Real	eps = `0.0`,
		const bool	single = `false`
	)

Constructor. Computes the global matrix by assembling the element matrices.

This constructor features a double loop over the elements of the image and the source space. On each combination, the bilinear form is called. You can force this constructor to execute the double loop in such a way that only for diagonal combinations of the elements in both space the integration and assembling is executed. Use single and set it to true.

Use this constructor, if spcX != spcY or if you have local matrices which express the interaction of the two elements., const Real eps = 0.0, const Real eps = 0.0

In non-symmetric FEM (eg. DGFEM), one has to solve A^T u = f. This constructor computes A and not A^T.

Parameters

spcX	Image space
spcY	Source space
seq	Flag on where the elements have to be built
bf	Bilinear form
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.
single	Diagonal parameter flag

◆ SparseMatrix() [6/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spcX,
		const Space< G > &	spcY,
		const BilinearForm< F, G > &	bf,
		const Sequence< ElementWithCell< G > * > &	seq,
		const Real	eps = `0.0`
	)

Constructor. Computes the global matrix by assembling the element matrices.

This constructor features a double loop over the elements of the image and the source space. On each combination, the bilinear form is called. You can force this constructor to execute the double loop in such a way that only for diagonal combinations of the elements in both space the integration and assembling is executed. Use single and set it to true.

Use this constructor, if spcX != spcY or if you have local matrices which express the interaction of the two elements., const Real eps = 0.0, const Real eps = 0.0

In non-symmetric FEM (eg. DGFEM), one has to solve A^T u = f. This constructor computes A and not A^T.

Parameters

spcX	Image space
spcY	Source space
bf	Bilinear form
seq	Sequence of elements to take into account for the Image space
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [7/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spc,
		const BilinearForm< F, G > &	bf,
		const Real	eps = `0.0`
	)

Constructor. Computes the global matrix by assembling the element matrices.

Parameters

spc	Image and source space
bf	Bilinear form
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [8/17]

template<class F >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< typename Realtype< F >::type > &	spc,
		const BilinearFormContainer< F >	bf,
		const Real	eps = `0.0`
	)

Constructor. Computes the global matrix by assembling the element matrices.

Parameters

spc	Image and source space
bf	bilinearform Container
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [9/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spc,
		const Sequence< bool > &	seq,
		const BilinearForm< F, G > &	bf,
		const Real	eps = `0.0`
	)

Constructor. Computes the global matrix by assembling the element matrices.

Parameters

spc	Image and source space
seq	Flag on where the elements have to be built
bf	Bilinear form
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [10/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spc,
		const BilinearForm< F, G > &	bf,
		const Sequence< ElementWithCell< G > * > &	seq,
		const Real	eps = `0.0`
	)

Constructor. Computes the partial matrix by assembling the element matrices on a given subdomain

Parameters

spc	Image and source space
bf	Bilinear form
seq	Sequence of elements to take into account
eps	entries, which absolute value is smaller then eps times the maximal absolute value of the element matrix are set to zero.

◆ SparseMatrix() [11/17]

template<class F >

concepts::SparseMatrix< F >::SparseMatrix	(	const SparseMatrix< F > &	m,
		bool	t = `false`
	)

Copy constructor. If t is set to true, the matrix is transposed during the copy process

◆ SparseMatrix() [12/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spc,
		const F *const	v,
		const int	i = `-1`
	)

Constructor of partial rank 1 matrix. The matrix is set to 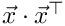$\vec x \cdot \vec x^\top$ where the bottom entries of x are given by v and, if i >= 0, x(i) = 1 and x(0:i) = 0.

Parameters

spc	Image and source space
v	Partial vector for rank 1 product
i	Shift index, `i==-1` means that v has the full size of x

◆ SparseMatrix() [13/17]

template<class F >

template<class G >

concepts::SparseMatrix< F >::SparseMatrix	(	const Space< G > &	spc,
		const Vector< F > &	x,
		const Vector< F > &	y
	)

Constructor of rank 1 matrix. The matrix is set to 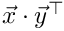$\vec x \cdot \vec y^\top$ .

Parameters

spc	Image and source space
x	First vector
y	Second vector

◆ SparseMatrix() [14/17]

template<class F >

template<class H >

concepts::SparseMatrix< F >::SparseMatrix	(	Operator< H > &	A,
		bool	slow = `false`
	)

Constructor. Converts A to a sparse matrix.

In case, the slow mode is allowed, the matrix is computed by multiplying A with the standard basis vectors and entering the results into the matrix. This is a O(n^2) operation.

Parameters

A	Operator to store as sparse matrix
slow	Also do slow O(n^2) conversion if nothing else is left.

◆ SparseMatrix() [15/17]

template<class F >

template<class H >

concepts::SparseMatrix< F >::SparseMatrix	(	const SparseMatrix< H > &	fncX,
		F	fncconst H &
	)

Constructor. Use this constructor to create a matrix of type F out of a matrix with entries of type H. The F type vector consists of elementwise evaluations of the function fnc.

Definition at line 482 of file sparseMatrix.hh.

◆ SparseMatrix() [16/17]

template<class F >

template<class H >

concepts::SparseMatrix< F >::SparseMatrix	(	const SparseMatrix< H > &	fncX,
		const F &	fncconst H &
	)

Definition at line 518 of file sparseMatrix.hh.

◆ SparseMatrix() [17/17]

template<class F >

template<class H >

concepts::SparseMatrix< F >::SparseMatrix ( const SparseMatrix< H > & fncX )

Constructor. Use this constructor to create a matrix of type F out of a matrix with entries of type H. The F type vector consists of elementwise conversions.

Definition at line 500 of file sparseMatrix.hh.

◆ ~SparseMatrix()

template<class F >

virtual concepts::SparseMatrix< F >::~SparseMatrix ( )

inlinevirtual

Definition at line 313 of file sparseMatrix.hh.

Member Function Documentation

◆ add() [1/2]

template<class F >

virtual void concepts::Matrix< F >::add	(	const uint	i,
		const uint	j,
		const F	value,
		const bool	use_threshold = `false`,
		const Real	threshold_value = `1e-8`
	)

virtualinherited

Addition operator Add the value to the entry (i,j) if not zero (for use_threshold = false), or if the absolute avlue is bigger than the threshold_value (for use_threshold = true)

◆ add() [2/2]

template<class F >

template<class H , class I >

void concepts::SparseMatrix< F >::add	(	const Vector< H > &	v,
		const I	fact,
		const uint	rowoffset = `0`,
		const uint	coloffset = `0`
	)

Copies the vector v multiplied by fact on position (rowoffset, coloffset)

Definition at line 597 of file sparseMatrix.hh.

◆ addInto()

template<class F >

template<class H , class I >

void concepts::SparseMatrix< F >::addInto	(	Matrix< H > &	dest,
		const I	fact,
		const uint	rowoffset = `0`,
		const uint	coloffset = `0`
	)		const

This matrix is added as block to the given matrix dest.

Parameters

dest	Matrix into which this matrix should be added.
fact	Factor by which this matrix should be multiplied.
rowoffset	Row in `dest`, where block begins.
coloffset	Column in `dest`, where block begins.

For example: Given a real matrix R. Then one construct a complex one by

SparseMatrix<Cmplx> C(spc,spc);
R.addInto(C, 1.0);

Examples: BGT_0.cc, RobinBCs.cc, exactDtN.cc, howToGetStarted.cc, hpFEM2d.cc, hpFEM3d-EV.cc, inhomDirichletBCs.cc, inhomDirichletBCsLagrange.cc, inhomNeumannBCs.cc, and parallelizationTutorial.cc.

Definition at line 538 of file sparseMatrix.hh.

◆ addIntoT()

template<class F >

template<class H , class I >

void concepts::SparseMatrix< F >::addIntoT	(	Matrix< H > &	dest,
		const I	fact,
		const uint	rowoffset = `0`,
		const uint	coloffset = `0`
	)		const

The transposed of this matrix is added as block to the given matrix.

Parameters

dest	Matrix into which this matrix should be added.
fact	Factor by which this matrix should be multiplied.
rowoffset	Row in `dest`, where block begins.
coloffset	Column in `dest`, where block begins.

Definition at line 567 of file sparseMatrix.hh.

◆ addT()

template<class F >

template<class H , class I >

void concepts::SparseMatrix< F >::addT	(	const Vector< H > &	v,
		const I	fact,
		const uint	rowoffset = `0`,
		const uint	coloffset = `0`
	)

Copies the transpose of the vector v multiplied by fact on position (rowoffset, coloffset)

Definition at line 613 of file sparseMatrix.hh.

◆ assembly() [1/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const BilinearForm< F, G > &	bf,
		const ElementPairList< G > &	pairs
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator uses the element pairs taken from pairs. For every two elements found in a ElementPair in pairs, the bilinear form is evaluated and the result assembled into dest.

◆ assembly() [2/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Sequence< ElementWithCell< G > * >	seq,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator does not compute element matrices for two different elements. The elements are taken from the element sequence seq.

◆ assembly() [3/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Sequence< ElementWithCell< G > * >	seqX,
		const Space< G > &	spcY,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator computes also the element matrices for two different elements. The elements are taken from the element sequence seqX for the test space, and the trial space spcY is fully taken into account.

◆ assembly() [4/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Space< G > &	spc,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator does not compute element matrices for two different elements. The elements are taken from the space spc.

Examples: linearDG1d.cc.

◆ assembly() [5/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Space< G > &	spc,
		const Sequence< bool > &	seq,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`
	)

staticinherited

Assembly operator for dest using the bilinear form bf on space spc. This assembly operator does not compute element matrices for two different elements. The elements are computing on the cells that are flagged by seq.

◆ assembly() [6/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Space< G > &	spcX,
		const Space< G > &	spcY,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`,
		const bool	single = `false`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator computes also the element matrices for two different elements (coming from test space spcX and trial space spcY).

◆ assembly() [7/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		const Space< G > &	spcX,
		const Space< G > &	spcY,
		const Sequence< bool > &	seq,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`,
		const bool	single = `false`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator computes also the element matrices for two different elements (coming from test space spcX and trial space spcY). The elements are computing on the cells that are flagged by seq.

◆ assembly() [8/8]

template<class F >

template<class G >

static void concepts::Matrix< F >::assembly	(	Matrix< F > &	dest,
		Scan< Element< G > > *	sc,
		const BilinearForm< F, G > &	bf,
		const Real	threshold = `0.0`
	)

staticinherited

Assembly operator for dest using the bilinear form bf. This assembly operator does not compute element matrices for two different elements. The elements are taken from the space scanner sc.

◆ begin() [1/2]

template<class F >

iterator concepts::SparseMatrix< F >::begin ( uint row = 0 )

Iterator over the elements, standing at position (row,c), where row is the given row number and c the first non-zero entry. If there is not entry in this line, the iterators stand at the next non-zero entry or it is end(), if the matrix is empty.

◆ begin() [2/2]

template<class F >

const_iterator concepts::SparseMatrix< F >::begin ( uint row = 0 ) const

Constant iterator over the elements, standing at position (row,c), where row is the given row number and c the first non-zero entry. If there is not entry in this line, the iterators stand at the next non-zero entry or it is end(), if the matrix is empty.

◆ compress()

template<class F >

void concepts::SparseMatrix< F >::compress ( Real threshold = EPS )

inline

Compresses the matrix by dropping small entries. All matrix entries which are smaller than a certain threshold times the largest entry of the matrix are deleted from the matrix.

Examples: RobinBCs.cc, hpFEM2d-simple.cc, hpFEM2d.cc, hpFEM3d-EV.cc, inhomDirichletBCs.cc, inhomDirichletBCsLagrange.cc, and inhomNeumannBCs.cc.

Definition at line 444 of file sparseMatrix.hh.

◆ convertCCS()

template<class F >

virtual void concepts::SparseMatrix< F >::convertCCS	(	F *	a,
		int *	asub,
		int *	xa
	)		const

virtual

Converts to Compressed Column Storage (CCS) format and writes values to field a, the row number asub and the index of the first value of each column xa. The fields have to be allocated with enough memory.

Implements concepts::CRSConvertable< F >.

◆ convertCRS()

template<class F >

virtual void concepts::SparseMatrix< F >::convertCRS	(	F *	a,
		int *	asub,
		int *	xa
	)		const

virtual

Converts to Compressed Row Storage (CRS) format and writes values to field a, the column number asub and the index of the first value of each row xa. The fields have to be allocated with enough memory.

Implements concepts::CRSConvertable< F >.

◆ convertIJK()

template<class F >

virtual void concepts::SparseMatrix< F >::convertIJK	(	F *	a,
		int *	irn,
		int *	jcn
	)		const

virtual

Convert to coordinate (COO) format and writes values to field a, the row indices to irn and the column indices to jcn. The fields have to be allocated with enough memory.

Implements concepts::CRSConvertable< F >.

◆ dimX()

template<class F >

virtual const uint concepts::Operator< F >::dimX ( ) const

inlinevirtualinherited

Returns the size of the image space of the operator (number of rows of the corresponding matrix)

Examples: hpFEM2d-simple.cc, hpFEM2d.cc, and matfileTutorial.cc.

Definition at line 93 of file compositions.hh.

◆ dimY()

template<class F >

virtual const uint concepts::Operator< F >::dimY ( ) const

inlinevirtualinherited

Returns the size of the source space of the operator (number of columns of the corresponding matrix)

Examples: matfileTutorial.cc.

Definition at line 98 of file compositions.hh.

◆ end()

template<class F >

iterator concepts::Matrix< F >::end ( )

inlineinherited

Iterator, standing behind last element.

Definition at line 66 of file matrix.hh.

◆ info()

template<class F >

virtual std::ostream & concepts::SparseMatrix< F >::info ( std::ostream & os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::Operator< F >.

◆ m()

template<class F >

const HashedSparseMatrix< F > * concepts::SparseMatrix< F >::m ( ) const

inline

Returns the sparse matrix itself.

Definition at line 378 of file sparseMatrix.hh.

◆ memory()

template<class F >

float concepts::SparseMatrix< F >::memory ( ) const

inline

Memory usage in byte.

Definition at line 435 of file sparseMatrix.hh.

◆ multiply() [1/2]

template<class F >

template<class H >

void concepts::SparseMatrix< F >::multiply	(	const H &	fact,
		Matrix< F > &	dest
	)		const

inline

Multiplies this matrix with fact and adds the result to dest.

Definition at line 429 of file sparseMatrix.hh.

◆ multiply() [2/2]

template<class F >

void concepts::SparseMatrix< F >::multiply	(	const SparseMatrix< F > &	fact,
		Matrix< F > &	dest
	)		const

inline

Multiplies this matrix with fact and adds the result to dest.

Definition at line 424 of file sparseMatrix.hh.

◆ nofCols()

template<class F >

const uint concepts::Matrix< F >::nofCols ( ) const

inlineinherited

Number of columns.

Definition at line 58 of file matrix.hh.

◆ nofRows()

template<class F >

const uint concepts::Matrix< F >::nofRows ( ) const

inlineinherited

Number of rows.

Definition at line 56 of file matrix.hh.

◆ operator()() [1/6]

template<class F >

virtual void concepts::Operator< F >::operator() ( )

virtualinherited

Application operator without argument

Reimplemented in concepts::BelosSolver< T >, concepts::VecOperator< F >, concepts::VecOperator< Cmplx >, concepts::VecOperator< F::d_type >, concepts::VecOperator< Real >, and concepts::VecOperator< T >.

◆ operator()() [2/6]

template<class F >

virtual void concepts::SparseMatrix< F >::operator()	(	const Function< c_type > &	fncY,
		Function< c_type > &	fncX
	)

virtual

Application operator for complex function fncY.

Computes fncX = A(fncY) where A is this operator. fncX becomes complex.

In derived classes its enough to implement the operator() for complex Operator's. If a real counterpart is not implemented, the function fncY is splitted into real and imaginary part and the application operator for real functions is called for each. Then the result is combined.

If in a derived class the operator() for complex Operator's is not implemented, a exception is thrown from here.

Implements concepts::Matrix< F >.

◆ operator()() [3/6]

template<class F >

virtual void concepts::Matrix< F >::operator()	(	const Function< r_type > &	fncY,
		Function< F > &	fncX
	)

pure virtualinherited

Computes fncX = A(fncY) where A is this matrix.

Reimplemented from concepts::Operator< F >.

Implemented in concepts::DenseMatrix< F >, concepts::DiagonalMatrix< F >, and concepts::Permutation< F >.

◆ operator()() [4/6]

template<class F >

virtual F & concepts::SparseMatrix< F >::operator()	(	const uint	i,
		const uint	j
	)

inlinevirtual

Returns and allows access to entry with indices i and j.

Implements concepts::Matrix< F >.

Definition at line 353 of file sparseMatrix.hh.

◆ operator()() [5/6]

template<class F >

virtual F concepts::SparseMatrix< F >::operator()	(	const uint	i,
		const uint	j
	)		const

inlinevirtual

Returns entry with indices i and j.

Implements concepts::Matrix< F >.

Definition at line 351 of file sparseMatrix.hh.

◆ operator()() [6/6]

template<class F >

template<class H , class I >

void concepts::SparseMatrix< F >::operator()	(	const Vector< H > &	fncY,
		Vector< I > &	fncX
	)

inline

Multiplies the matrix with fncY. The result is fncX.

Definition at line 322 of file sparseMatrix.hh.

◆ operator*=()

template<class F >

SparseMatrix< F > & concepts::SparseMatrix< F >::operator*= ( const F factor )

inline

Definition at line 355 of file sparseMatrix.hh.

◆ operator==()

template<class F >

virtual bool concepts::Matrix< F >::operator== ( const Matrix< F > & otherMat ) const

inlinevirtualinherited

Definition at line 179 of file matrix.hh.

◆ resize()

template<class F >

virtual void concepts::SparseMatrix< F >::resize	(	uint	m,
		uint	n
	)

inlinevirtual

Sets a new size, previous data might be lost

Definition at line 361 of file sparseMatrix.hh.

◆ set()

template<class F >

virtual void concepts::Matrix< F >::set	(	const uint	i,
		const uint	j,
		const F	value,
		const bool	use_threshold = `false`,
		const Real	threshold_value = `1e-8`
	)

virtualinherited

Affectation operator Affet the value to the entry (i,j) if not zero (for use_threshold = false), or if the absolute value is bigger than the threshold_value (for use_threshold = true)

◆ setTimings()

template<class F >

static void concepts::Matrix< F >::setTimings ( InOutParameters * timings )

staticinherited

Sets the class to store the timing values in. Additionally, the timeCntr_ is reset to 0. This counter is used to fill in the values into the arrays listed below in subsequent calls. The following timings are taken and stored in timings:

evaluation of bilinear form in bilinear_form
application of T matrix in tmatrix_apply
assembling into global matrix in global_assembly

◆ show_messages()

template<class F >

virtual void concepts::Operator< F >::show_messages ( )

inlinevirtualinherited

Reimplemented in concepts::MumpsOverlap< F >.

Definition at line 100 of file compositions.hh.

◆ storeMatlab()

template<class F >

bool concepts::SparseMatrix< F >::storeMatlab	(	const std::string	filename,
		const std::string	name = `""`,
		bool	append = `false`
	)		const

Stores the matrix in a Matlab sparse matrix

Returns: true if the writes was successfull

◆ timings()

template<class F >

static bool concepts::Matrix< F >::timings ( )

staticinherited

Returns true if the class is able to do timings. The ability to do timings depends on a compiler switch in matrix.cc file.

◆ transpMult() [1/3]

template<class F >

virtual void concepts::SparseMatrix< F >::transpMult	(	const Vector< c_type > &	fncY,
		Vector< c_type > &	fncX
	)

virtual

Implements concepts::Matrix< F >.

◆ transpMult() [2/3]

template<class F >

virtual void concepts::SparseMatrix< F >::transpMult	(	const Vector< r_type > &	fncY,
		Vector< F > &	fncX
	)

virtual

Multiplies the transpose of the matrix with fncY and adds the results to fncX.

◆ transpMult() [3/3]

template<class F >

virtual void concepts::Matrix< F >::transpMult	(	const Vector< r_type > &	fncY,
		Vector< F > &	fncX
	)

pure virtualinherited

Computes fncX = A^T fncY where A is this matrix.

Implemented in concepts::DenseMatrix< F >, concepts::DiagonalMatrix< F >, and concepts::Permutation< F >.

◆ used()

template<class F >

virtual uint concepts::SparseMatrix< F >::used ( ) const

inlinevirtual

Returns the number of used entries in the matrix.

Implements concepts::CRSConvertable< F >.

Definition at line 433 of file sparseMatrix.hh.

◆ write()

template<class F >

void concepts::SparseMatrix< F >::write ( char * fname ) const

Writes the matrix to a file.

Parameters

fname Filename

Member Data Documentation

◆ dimX_

template<class F >

uint concepts::Operator< F >::dimX_

protectedinherited

Dimension of image space and the source space.

Definition at line 104 of file compositions.hh.

◆ dimY_

template<class F >

uint concepts::Operator< F >::dimY_

protectedinherited

Definition at line 104 of file compositions.hh.

The documentation for this class was generated from the following files:

operator/compositions.hh
operator/sparseMatrix.hh

Class documentation of Concepts

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Member Typedef Documentation

◆ c_type

◆ const_iterator

◆ d_type

◆ iterator

◆ r_type

◆ type

◆ value_type

Constructor & Destructor Documentation

◆ SparseMatrix() [1/17]

◆ SparseMatrix() [2/17]

◆ SparseMatrix() [3/17]

◆ SparseMatrix() [4/17]

◆ SparseMatrix() [5/17]

◆ SparseMatrix() [6/17]

◆ SparseMatrix() [7/17]

◆ SparseMatrix() [8/17]

◆ SparseMatrix() [9/17]

◆ SparseMatrix() [10/17]

◆ SparseMatrix() [11/17]

◆ SparseMatrix() [12/17]

◆ SparseMatrix() [13/17]

◆ SparseMatrix() [14/17]

◆ SparseMatrix() [15/17]

◆ SparseMatrix() [16/17]

◆ SparseMatrix() [17/17]

◆ ~SparseMatrix()

Member Function Documentation

◆ add() [1/2]

◆ add() [2/2]

◆ addInto()

◆ addIntoT()

◆ addT()

◆ assembly() [1/8]

◆ assembly() [2/8]

◆ assembly() [3/8]

◆ assembly() [4/8]

◆ assembly() [5/8]

◆ assembly() [6/8]

◆ assembly() [7/8]

◆ assembly() [8/8]

◆ begin() [1/2]

◆ begin() [2/2]

◆ compress()

◆ convertCCS()

◆ convertCRS()

◆ convertIJK()

◆ dimX()

◆ dimY()

◆ end()

◆ info()

◆ m()

◆ memory()

◆ multiply() [1/2]

◆ multiply() [2/2]

◆ nofCols()

◆ nofRows()

◆ operator()() [1/6]

◆ operator()() [2/6]

◆ operator()() [3/6]

◆ operator()() [4/6]

◆ operator()() [5/6]

◆ operator()() [6/6]

◆ operator*=()

◆ operator==()

◆ resize()

◆ set()

◆ setTimings()

◆ show_messages()

◆ storeMatlab()

◆ timings()

◆ transpMult() [1/3]

◆ transpMult() [2/3]