Class documentation of Concepts
#include <bilinearFormHelper.hh>

Public Member Functions | |
| BilinearFormHelper_1_1 (const concepts::ElementFormulaContainer< F > frm) | |
| Constructor for scalar function. | |
| BilinearFormHelper_1_1 (const concepts::ElementFormulaContainer< concepts::Mapping< G, 2 > > frmM) | |
| Constructor for matrix valued function. | |
| virtual | ~BilinearFormHelper_1_1 () |
| Destructor. | |
| void | data (const concepts::RCP< concepts::SharedJacobianAdj< 2 > > d) |
| Set the pointer to the shared data. | |
| concepts::RCP< concepts::SharedJacobianAdj< 2 > > | data () const |
| Gets the pointer to the shared data. | |
Protected Member Functions | |
| void | computeIntermediate_ (const BaseQuad< Real > &elm, const int i=-1, const int j=-1) const |
Protected Attributes | |
| concepts::Array< F > | intermediateValue_ |
| concepts::Array< concepts::Mapping< G, 2 > > | intermediateMatrix_ |
| concepts::ElementFormulaContainer< F > | frm_ |
| Element formula. | |
| concepts::ElementFormulaContainer< concepts::Mapping< G, 2 > > | frmM_ |
| Matrix element formula. | |
Detailed Description
class hp2D::BilinearFormHelper_1_1< F, G >
Helper class for bilinearforms a(u,v), where u and v are 1-forms, which computes intermediate data for element matrix computation.
It works with scalar functions and matrix valued functions.
For scalar function 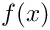
![\[\displaystyle a(u,v) = \int\limits_K f(x)\underline{u}^T\underline{v}\,dx = \int\limits_{\hat{K}} \hat{\underline{u}}\,\circ F_K^{-1}J^{-1}J^{-\top}\hat{\underline{v}}\,\circ F_K^{-1}f(F_K(\xi))\det J\,d\xi = \int\limits_{\hat{K}} \hat{\underline{u}}\,\circ F_K^{-1}\mbox{adj}(J)\mbox{adj}(J)^\top\hat{\underline{v}}\,\circ F_K^{-1}\frac{f(F_K(\xi))}{\det J}\,d\xi\]](form_505.png)
For matrix valued function 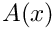
![\[\displaystyle a(u,v) = \int\limits_K \underline{u}^TA(x)\underline{v}\,dx = \int\limits_{\hat{K}} \hat{\underline{u}}\,\circ F_K^{-1}J^{-1}A(F_K(\xi))J^{-\top}\hat{\underline{v}}\,\circ F_K^{-1}\det J\,d\xi = \int\limits_{\hat{K}} \hat{\underline{u}}\,\circ F_K^{-1}\mbox{adj}(J)A(F_K(\xi))\mbox{adj}(J)^\top\hat{\underline{v}}\,\circ F_K^{-1}\frac{1}{\det J}\,d\xi\]](form_507.png)
For scalar functions also the intermediate data for a bilinear form with partial derivatives can be stored, where the intermediate matrix is the rank-1 product of j-th column of 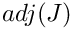
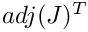
Here, J is the Jacobian matrix.
The adjunct of the Jacobian matrix and the inverse of the determinant of the Jacobian matrix can be shared between different instances of the class. This is useful for bilinear forms on vectorial spaces.
Definition at line 140 of file bilinearFormHelper.hh.
Member Function Documentation
◆ computeIntermediate_()
|
protected |
Compute the intermediate data for element matrix computation.
- Parameters
-
i if i=0 or 1, then take only i-th column of Jacobian matrix (for test function) j if j=0 or 1, then take only j-th column of Jacobian matrix (for trial function)
The Jacobian matrices have to been taken both full (i,j = -1) or both partial (i,j = 0 or 1).
Matrix formulas and complex valued scalar formulas are only implemented for full Jacobians.
Member Data Documentation
◆ frm_
|
protected |
Element formula.
Definition at line 193 of file bilinearFormHelper.hh.
◆ frmM_
|
protected |
Matrix element formula.
Definition at line 195 of file bilinearFormHelper.hh.
◆ intermediateMatrix_
|
mutableprotected |
Intermediate matrix
In case of a scalar formula:
![\[\mbox{adj}(J) \mbox{adj}(J)^\top\]](form_517.png)
In case of a matrix formula 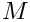
![\[\mbox{adj}(J) M \mbox{adj}(J)^\top\]](form_518.png)
In case of partial Jacobian:
![\[\mbox{adj}(J)_{\cdot,j} (\mbox{adj}(J)_{\cdot,i})^\top\]](form_519.png)
Definition at line 191 of file bilinearFormHelper.hh.
◆ intermediateValue_
|
mutableprotected |
Intermediate value
In case of a scalar formula:
![\[\frac{f(F_K(\xi))}{\det J}\]](form_515.png)
In case of a matrix formula:
![\[\frac{1}{\det J}\]](form_516.png)
Definition at line 179 of file bilinearFormHelper.hh.
The documentation for this class was generated from the following file:
Generated on Wed Sep 13 2023 21:06:52 for Concepts by
