Class documentation of Concepts
#include <bf_graduv.hh>

Public Types | |
| typedef concepts::Combtype< F, G >::type | value_type |
Public Member Functions | |
| GraduvBase (const concepts::ElementFormulaContainer< F > frm, bool all=false) | |
| GraduvBase (const concepts::ElementFormulaContainer< concepts::Mapping< G, 2 > > frm, bool all=false) | |
| void | data (const concepts::RCP< concepts::SharedJacobianAdj< 2 > > d) |
| Set the pointer to the shared data. | |
| concepts::RCP< concepts::SharedJacobianAdj< 2 > > | data () const |
| Gets the pointer to the shared data. | |
Protected Member Functions | |
| bool | assemble_ (const hp2D::Quad< Real > *elmX, const Quad< Real > *elmY, concepts::ElementMatrix< value_type > &em) const |
| void | computeIntermediate_ (const BaseQuad< Real > &elm, const int i=-1, const int j=-1) const |
Protected Attributes | |
| bool | all_ |
| Parameter for the sum factorisation. | |
| concepts::Array< F > | intermediateValue_ |
| concepts::Array< concepts::Mapping< G, 2 > > | intermediateMatrix_ |
| concepts::ElementFormulaContainer< F > | frm_ |
| Element formula. | |
| concepts::ElementFormulaContainer< concepts::Mapping< G, 2 > > | frmM_ |
| Matrix element formula. | |
Detailed Description
class hp2Dedge::GraduvBase< F, G >
Base class to calculate element matrices for the (grad u, v)-bilinearform, for both scalar and matrix formulas.
This class is inspired by hp2D::LaplaceBase.
Definition at line 63 of file bf_graduv.hh.
Member Typedef Documentation
◆ value_type
| typedef concepts::Combtype<F,G>::type hp2Dedge::GraduvBase< F, G >::value_type |
Definition at line 66 of file bf_graduv.hh.
Constructor & Destructor Documentation
◆ GraduvBase()
| hp2Dedge::GraduvBase< F, G >::GraduvBase | ( | const concepts::ElementFormulaContainer< F > | frm, |
| bool | all = false |
||
| ) |
Constructor. The formula frm is evaluated in each quadrature point.
Member Function Documentation
◆ computeIntermediate_()
|
protectedinherited |
Compute the intermediate data for element matrix computation.
- Parameters
-
i if i=0 or 1, then take only i-th column of Jacobian matrix (for test function) j if j=0 or 1, then take only j-th column of Jacobian matrix (for trial function)
The Jacobian matrices have to been taken both full (i,j = -1) or both partial (i,j = 0 or 1).
Matrix formulas and complex valued scalar formulas are only implemented for full Jacobians.
Member Data Documentation
◆ all_
|
protected |
Parameter for the sum factorisation.
Definition at line 79 of file bf_graduv.hh.
◆ frm_
|
protectedinherited |
Element formula.
Definition at line 193 of file bilinearFormHelper.hh.
◆ frmM_
|
protectedinherited |
Matrix element formula.
Definition at line 195 of file bilinearFormHelper.hh.
◆ intermediateMatrix_
|
mutableprotectedinherited |
Intermediate matrix
In case of a scalar formula:
![\[\mbox{adj}(J) \mbox{adj}(J)^\top\]](form_517.png)
In case of a matrix formula 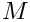
![\[\mbox{adj}(J) M \mbox{adj}(J)^\top\]](form_518.png)
In case of partial Jacobian:
![\[\mbox{adj}(J)_{\cdot,j} (\mbox{adj}(J)_{\cdot,i})^\top\]](form_519.png)
Definition at line 191 of file bilinearFormHelper.hh.
◆ intermediateValue_
|
mutableprotectedinherited |
Intermediate value
In case of a scalar formula:
![\[\frac{f(F_K(\xi))}{\det J}\]](form_515.png)
In case of a matrix formula:
![\[\frac{1}{\det J}\]](form_516.png)
Definition at line 179 of file bilinearFormHelper.hh.
The documentation for this class was generated from the following file:
- hp2Dedge/bf_graduv.hh
Generated on Wed Sep 13 2023 21:06:55 for Concepts by
