hp3D::DivDiv< Weight > Class Template Reference

#include <divdiv.hh>

Inheritance diagram for hp3D::DivDiv< Weight >:

Public Member Functions
	DivDiv (SingularSet &singularities, const uint i=0, const uint j=0, const concepts::Formula< Real > *frm=0)
	DivDiv (concepts::Array< Real > &jacobian, concepts::Array< concepts::MapReal3d > &jacobianInv, const Hexahedron **oldElm, SingularSet &singularities, const uint i=0, const uint j=0, const concepts::Formula< Real > *frm=0)
virtual DivDiv *	clone () const
virtual void	operator() (const concepts::Element< Real > &elmX, const concepts::Element< Real > &elmY, concepts::ElementMatrix< Real > &em) const
void	operator() (const Hexahedron &elmX, const Hexahedron &elmY, concepts::ElementMatrix< Real > &em) const
virtual void	data (concepts::Cloneable *d)
	Sets the data to be shared.
virtual MaxwellSharedData *	data () const
	Returns the data to be shared.
virtual void	operator() (const Element< typename Realtype< Real >::type > &elmX, const Element< typename Realtype< Real >::type > &elmY, ElementMatrix< Real > &em) const=0
virtual void	operator() (const Element< typename Realtype< Real >::type > &elmX, const Element< typename Realtype< Real >::type > &elmY, ElementMatrix< Real > &em, const ElementPair< typename Realtype< Real >::type > &ep) const

Static Public Member Functions
static void	setup (vectorial::BilinearForm< Real, Real > &bf, hp3D::SingularSet &singularities, const concepts::Formula< Real > *frm=0)

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

template<class Weight = TrivialWeight>
class hp3D::DivDiv< Weight >

A function class to calculate element matrices for the Div u*Div v Bilinearform.

The Jacobian, its inverse and additional quantities only depending on the physical coordinates are only computed once for all components of the bilinear form. To this end, several additional parameters can be given to the constructor (see there). However, it is much simpler to use the DivDiv::setup method which sets up everything automatically.

Author

Kersten Schmidt, 2002

Definition at line 46 of file divdiv.hh.

Constructor & Destructor Documentation

DivDiv() [1/2]

template<class Weight = TrivialWeight>

hp3D::DivDiv< Weight >::DivDiv	(	SingularSet &	singularities,
		const uint	i = 0,
		const uint	j = 0,
		const concepts::Formula< Real > *	frm = 0
	)

Constructor

Parameters

singularities	List of singular edges and vertices.
i	Index of the bilinear form in the vector valued bilinear form
j	Index of the bilinear form in the vector valued bilinear form
frm	Formula for the dielectricity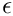

DivDiv() [2/2]

template<class Weight = TrivialWeight>

hp3D::DivDiv< Weight >::DivDiv	(	concepts::Array< Real > &	jacobian,
		concepts::Array< concepts::MapReal3d > &	jacobianInv,
		const Hexahedron **	oldElm,
		SingularSet &	singularities,
		const uint	i = 0,
		const uint	j = 0,
		const concepts::Formula< Real > *	frm = 0
	)

Constructor

Parameters

jacobian	Reference to the storage space for the Jacobian. Here, also other quantities are stored (premultiplied).
jacobianInv	Reference to the storage space for the inverse of the Jacobian.
oldElm	Pointer to the element of the last invocation to detect if the information in jacobian and jacobianInv is still valid.
singularities	List of singular edges and vertices.
i	Index of the bilinear form in the vector valued bilinear form
j	Index of the bilinear form in the vector valued bilinear form
frm	Formula for the dielectricity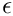

Member Function Documentation

clone()

template<class Weight = TrivialWeight>

virtual DivDiv * hp3D::DivDiv< Weight >::clone ( ) const

virtual

Virtual constructor. Returns a pointer to a copy of itself. The caller is responsible to destroy this copy.

Implements concepts::BilinearForm< Real >.

data() [1/2]

template<class Weight = TrivialWeight>

virtual MaxwellSharedData * hp3D::DivDiv< Weight >::data ( ) const

virtual

Returns the data to be shared.

Implements vectorial::Vectorizable.

data() [2/2]

template<class Weight = TrivialWeight>

virtual void hp3D::DivDiv< Weight >::data ( concepts::Cloneable *  )

virtual

Sets the data to be shared.

Implements vectorial::Vectorizable.

info()

template<class Weight = TrivialWeight>

virtual std::ostream & hp3D::DivDiv< Weight >::info ( std::ostream &  os ) const

protectedvirtual

Returns information in an output stream.

Reimplemented from concepts::BilinearForm< Real >.

operator()() [1/2]

virtual void concepts::BilinearForm< Real , typename Realtype<Real >::type >::operator() ( const Element< typename Realtype<Real >::type > &  elmX, const Element< typename Realtype<Real >::type > &  elmY, ElementMatrix< Real > &  em  ) const

pure virtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element (test functions)
elmY	Right element (trial functions)
em	Return element matrix

operator()() [2/2]

virtual void concepts::BilinearForm< Real , typename Realtype<Real >::type >::operator() ( const Element< typename Realtype<Real >::type > &  elmX, const Element< typename Realtype<Real >::type > &  elmY, ElementMatrix< Real > &  em, const ElementPair< typename Realtype<Real >::type > &  ep  ) const

inlinevirtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em. If this method is not reimplemented in a derived class, the default behaviour is to call the application operator without ep.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element
elmY	Right element
em	Return element matrix
ep	Element pair holding more information on the pair elmX and elmY

Definition at line 57 of file bilinearForm.hh.

setup()

template<class Weight = TrivialWeight>

static void hp3D::DivDiv< Weight >::setup ( vectorial::BilinearForm< Real, Real > &  bf, hp3D::SingularSet &  singularities, const concepts::Formula< Real > *  frm = 0  )

static

Sets up the bilinear form for the div-div part for Maxwell's equation using weighted regularization.

Parameters

bf	Resulting bilinear form (use this to compute the matrix)
singularities	Singularities needed for computing the weight
frm	Formula for the dielectricity (if none is given, 1 is assumed)

Precondition

The number of components of bf needs to be 3 x 3.

Examples

hpFEM3d-EV.cc.

---

The documentation for this class was generated from the following file:

• hp3D/divdiv.hh