You are here: Concepts>Concepts Web>Class documentation

Class documentation of Concepts

Searching...

No Matches

On this page you find the easy example of an elliptic partial differential equation that was already discussed in How to get started. However, in this tutorial the PDE is solved in parallel.

Introduction

Recall that the model problem is to find a finite element approximation to the unique solution 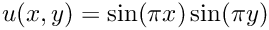$u(x,y) = \sin(\pi x) \sin(\pi y)$ of the following elliptic PDE with homogeneous Dirichlet boundary conditions

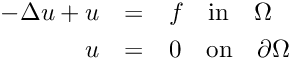
$\begin{eqnarray*} - \Delta u + u &=& f \quad \textrm{in} \quad \Omega\\ u &=& 0 \quad \textrm{on} \quad \partial \Omega\ \end{eqnarray*}$

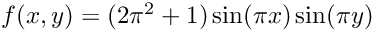
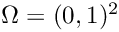
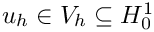
with the right hand side $f(x,y) = (2 \pi^2 +1)\sin(\pi x) \sin(\pi y)$ and $\Omega = (0,1)^2$ . The discrete variational formulation of this PDE reads: find $u_h \in V_h \subseteq H_0^1$ such that

$\int_{\Omega} \nabla u_h \cdot \nabla v_h \, {\rm d}\mathbf{x} + \int_\Omega u_h v_h \, {\rm d}\mathbf{x} = \int_\Omega f v_h {\rm d}\mathbf{x} \qquad \forall v_h \in V_h.$

Differences to the sequential version

If you are familiar with the sequential version, there are only some minors changes to apply.

Use MPI

The program should start with

@code
MPI_Init(&argc, &argv);
@endcode

and end with

@code
MPI_Finalize();
@endcode

In addition, we have to retrieve the number of processes using the command MPI_Comm_size and the current process using the command MPI_Comm_rank. By convention, the master process is the process of rank 0.

@code
int nbParts; MPI_Comm_size(MPI_COMM_WORLD, &nbParts);
int part; MPI_Comm_rank(MPI_COMM_WORLD, &part);
bool master = (part == 0);
@endcode

Graph partitioning

The graph partitioning is done with the generic concepts::SpaceGraph class.

@code
#include "space.hh"
concepts::SpaceGraph<hp2D::hpAdaptiveSpaceH1> sgraph(space);
sgraph.SplitGraph(nbParts);
@endcode

Matrix assembling

For the matrix assembling, we have to use the getSubDomain method as an additional parameter.

For example, we replace the build of the stiffness matrix 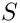and mass matrix

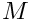
@code
concepts::SparseMatrix<Real> S(space, la);
concepts::SparseMatrix<Real> M(space, id);
@endcode

by the following builds

@code
concepts::SparseMatrix<Real> S(space, la, sgraph.getSubDomain(part));
concepts::SparseMatrix<Real> M(space, id, sgraph.getSubDomain(part));
@endcode

Solving process

The solving process does not differ very much from what is done in the sequential version. However, we have to use the concepts::MumpsOverlap class for solving.

We declare for each process the solver

@code
concepts::MumpsOverlap<Real>* solver = new concepts::MumpsOverlap<Real>(S, part);
@endcode

and we differentiate two cases:

If the process is the master process, we build the right hand side, solve and do the post-processing of the solution as usual.
If, on the other hand, the process is not the master process, we simply call the solver.

The associated code is

@code
if (master)
{
... Treatment before calling solver
(*solver)(rhs, sol);
... Treatment after calling solver
}
else
{
(*solver)();
}
@endcode

Commented Program

Now let us see how to parallelly calculate the FEM-approximation to the solution of the PDE with Concepts. First we have to include some headers to use the functions of specific Concepts packages.

#include "hp2D.hh"
#include "operator.hh"
#include "formula.hh"
#include "graphics.hh"
#include <mpi.h>
#include "space.hh"

The package hp2D includes all functions that are needed to build a representation of the hp-finite element space in two dimensions. The package operator.hh includes the data structures for Concepts matrices and linear solvers, the package formula allows you to represent the right hand side via its symbolic formula and the package graphics is used for the graphical output of the mesh and the solution.

The instruction

using concepts::Real;

concepts::Real

double Real

Definition typedefs.hh:39

allows us to use the datatype concepts::Real just by typing Real .

Next we start with the actual code, consisting of a main program.

int main(int argc, char** argv)

Since we use MPI, we also have to initialize the MPI process using the instruction MPI_Init .

MPI_Init(&argc, &argv);

First, we load the geometry that contains several cells.

  concepts::Import2dMesh
    mesh(SOURCEDIR "/applications/unitsquareCoordinates.dat",
         SOURCEDIR "/applications/unitsquareElements.dat",
         SOURCEDIR "/applications/unitsquareEdges.dat");

Now we prescribe homogeneous Dirichlet boundary conditions to all edges of attributes 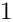to , i.e. to all edges.

  concepts::BoundaryConditions bc;
  for (uint i = 1; i <= 4; ++i)
    bc.add(concepts::Attribute(i), concepts::Boundary(concepts::Boundary::DIRICHLET));

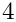
With the mesh and the boundary conditions at hand we can build the hp-finite element space.

  uint levelOfRefinement = 2;
  uint polynomialDegree = 6;
  hp2D::hpAdaptiveSpaceH1 space(mesh,levelOfRefinement,polynomialDegree,&bc);
  space.rebuild();

This is a finite element space on the square, with a twice refined mesh (a single refinement of a two dimensional mesh divides an element in the mesh into four elements, so in our case we have 16 subelements in our square) and polynomial degree six on every element.

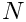
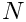
Now we split the graph associated to this mesh into parts, where is the number of MPI process given by the command mpirun -np N

  concepts::SpaceGraph<hp2D::hpAdaptiveSpaceH1> sgraph(space);
  int nbParts; MPI_Comm_size(MPI_COMM_WORLD, &nbParts);
  int part; MPI_Comm_rank(MPI_COMM_WORLD, &part);
  bool master = (part == 0);
  sgraph.SplitGraph(nbParts);

and we build the matrices S (the stiffness matrix, corresponding to the 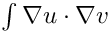$\int \nabla u \cdot \nabla v$ term) and M (the mass matrix, corresponding to the 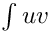$\int u v$ term)

  hp2D::Laplace<Real> la;
  hp2D::Identity<Real> id;
 
  // compute the mass and stiffness matrices
  // parallel: get part of the matrix corresponding to the subdomain
  concepts::SparseMatrix<Real> S(space, la, sgraph.getSubDomain(part));
  concepts::SparseMatrix<Real> M(space, id, sgraph.getSubDomain(part));
 
  // add mass matrix to stiffness matrix
  M.addInto(S, 1.);

Next point is that we build the solver (more precisely: the subpart of the solver corresponding to each thread)

  concepts::MumpsOverlap<Real>* solver = new concepts::MumpsOverlap<Real>(S, part);
 
  // define the solution vector
  concepts::Vector<Real> sol(space);
 
  MPI_Barrier(MPI_COMM_WORLD);

The treatment of the right hand side and the way we call the solver now depend on whether or not we are on the master thread.

if (master)

On the master thread, we build the right hand side and we call the solver.

      concepts::ParsedFormula<> f("((2*pi*pi+1)*sin(pi*x)*sin(pi*y))");
      hp2D::Riesz<Real> lform(f);
      
      // compute the vector for the finite element discretization
      concepts::Vector<Real> rhs(space, lform);
      
      // compute the solution
      (*solver)(rhs, sol);

On all other threads, we simply call the solver.

(*solver)();

Now we want to compute the error between the computed and the exact solution of PDE. Also this task can be done in parallel. Next we distribute the solution vector to all other threads.

MPI_Bcast(sol.data(), sol.size(), MPI_DOUBLE, 0, MPI_COMM_WORLD);

The formulas of computed and exact solution are build by

  hp2D::Value<Real> hp2Dvalue;
 
  // build the element formula from the solution vector
  concepts::ElementFormulaVector<1,Real> elmFormVector(space, sol, hp2Dvalue);  
 
  // define exact solution of the problem
  concepts::ParsedFormula<Real> exactSolution("(sin(4*atan(1.0)*x)*sin(4*atan(1.0)*y))");

Next we compute the 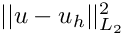$||u - u_h||^2_{L_2}$ on each subdomain.

Real L2productValue_task = concepts::L2product(sgraph.getSubDomain(part), elmFormVector-exactSolution );

concepts::L2product

Real L2product(const ElementWithCell< G > &elm, const ElementFormula< F, G > &u, const ElementFormula< Real > *c=0, const Real t=0.0, IntegrationCell::intFormType form=IntegrationCell::ZERO)

Definition integral.hh:214

Finally we collect the values from all threads

Real L2productResult(0);

MPI_Allreduce(&L2productValue_task, &L2productResult, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);

Complete Source Code

 
#include "hp2D.hh"
#include "operator.hh"
#include "formula.hh"
#include "graphics.hh"
#include <mpi.h>
#include "space.hh"
 
using concepts::Real;
 
int main(int argc, char** argv)
{
 
  // parallel: initialize MPI session
  MPI_Init(&argc, &argv);
 
  // import 2D mesh
  concepts::Import2dMesh
    mesh(SOURCEDIR "/applications/unitsquareCoordinates.dat",
         SOURCEDIR "/applications/unitsquareElements.dat",
         SOURCEDIR "/applications/unitsquareEdges.dat");
 
  // set homogeneous Dirichlet boundary conditions for every edge of attribute 1-4 (i.e. all edges) 
  concepts::BoundaryConditions bc;
  for (uint i = 1; i <= 4; ++i)
    bc.add(concepts::Attribute(i), concepts::Boundary(concepts::Boundary::DIRICHLET));
 
 
  // build the finite element space V_2_6
  uint levelOfRefinement = 2;
  uint polynomialDegree = 6;
  hp2D::hpAdaptiveSpaceH1 space(mesh,levelOfRefinement,polynomialDegree,&bc);
  space.rebuild();
 
  // parallel: split graph
  concepts::SpaceGraph<hp2D::hpAdaptiveSpaceH1> sgraph(space);
  int nbParts; MPI_Comm_size(MPI_COMM_WORLD, &nbParts);
  int part; MPI_Comm_rank(MPI_COMM_WORLD, &part);
  bool master = (part == 0);
  sgraph.SplitGraph(nbParts);
 
  // define the bilinear forms
  hp2D::Laplace<Real> la;
  hp2D::Identity<Real> id;
 
  // compute the mass and stiffness matrices
  // parallel: get part of the matrix corresponding to the subdomain
  concepts::SparseMatrix<Real> S(space, la, sgraph.getSubDomain(part));
  concepts::SparseMatrix<Real> M(space, id, sgraph.getSubDomain(part));
 
  // add mass matrix to stiffness matrix
  M.addInto(S, 1.);
 
  // compute the solution of the linear problem using the mumps solver
  // with overlap
  concepts::MumpsOverlap<Real>* solver = new concepts::MumpsOverlap<Real>(S, part);
 
  // define the solution vector
  concepts::Vector<Real> sol(space);
 
  MPI_Barrier(MPI_COMM_WORLD);
  if (master)
    {
      // define the linear form f of the right hand side
      concepts::ParsedFormula<> f("((2*pi*pi+1)*sin(pi*x)*sin(pi*y))");
      hp2D::Riesz<Real> lform(f);
      
      // compute the vector for the finite element discretization
      concepts::Vector<Real> rhs(space, lform);
      
      // compute the solution
      (*solver)(rhs, sol);
      
    }
  else
    {
      // call the solver on all other threads
      (*solver)();
    }
 
  MPI_Barrier(MPI_COMM_WORLD);
  
  // distribute the solution vector to all other threads
  MPI_Bcast(sol.data(), sol.size(), MPI_DOUBLE, 0, MPI_COMM_WORLD); 
 
  // define an element function
  hp2D::Value<Real> hp2Dvalue;
 
  // build the element formula from the solution vector
  concepts::ElementFormulaVector<1,Real> elmFormVector(space, sol, hp2Dvalue);  
 
  // define exact solution of the problem
  concepts::ParsedFormula<Real> exactSolution("(sin(4*atan(1.0)*x)*sin(4*atan(1.0)*y))");
 
  // compute the square of L2-Norm of the error on each subdomain
  Real L2productValue_task = concepts::L2product(sgraph.getSubDomain(part), elmFormVector-exactSolution );
 
  // collect the values from all threads
  Real L2productResult(0);
  MPI_Allreduce(&L2productValue_task, &L2productResult, 1, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
 
  // postprocessing
  if (master) 
    {
      std::cout<<"L2 error=" << sqrt(L2productResult)<<std::endl;
 
      // set integration points to be equidistant using trapezoidal rule
      hp2D::IntegrableQuad::factory().get()->setTensor(concepts::TRAPEZE, true,
                                                       polynomialDegree);
      space.recomputeShapefunctions();
      
      // save graphical output of the solution in a MAT-file
      graphics::MatlabBinaryGraphics mbg(space, "firstSolution");
      mbg.addSolution(space, "u", sol);
    }
 
  // parallel: close MPI session
 
  MPI_Finalize();
 
  return 0;
}
 