Class documentation of Concepts
#include <elementMaps3D.hh>
Public Member Functions | |
| MapTetrahedron3d (char *map, Real scX, Real scY, Real scZ) | |
| MapTetrahedron3d (Real3d vtx0, Real3d vtx1, Real3d vtx2, Real3d vtx3) | |
| MapTetrahedron3d (const MapTetrahedron3d &map) | |
| Copy constructor. | |
| Real3d | operator() (Real x, Real y, Real z) const |
| Real | jacobian () const |
| Returns the jacobian. | |
| MapTetrahedron3d * | clone () const |
| Returns a copy of the map. | |
| std::ostream & | info (std::ostream &os) const |
| Returns information in an output stream. | |
Detailed Description
A 3D element map for a tetrahedron. The reference element is the unit cube.
There are two ways to fix the map of the tetrahedron: give the mapping explicitly or give the four corners and the map is computed internally.
Giving the map explicitly needs a few precautions: The reference element is the unit cube. For easier construction of the element map, a rectangle ![$[0,a] \times [0,b] \times [0,c]$](form_328.png)
With a arbitrary Duffy transformation, one can choose the side which sould collapse. Here, the top face of the cube and the back edge of the bottom face should degenerate to a point, ie. the unit cube maps onto the unit simplex. This can be done with three Duffy transformations:
- Collapse the top face against the 2 direction.
- Collapse the resulting egde against the 1 direction.
- Collapse the back edge of the bottom face against the 1 direction.
When giving the four corners, the first three have to be in the normal orientation of the first triangle of the tetrahedron, see Tetrahedron for the explanation of "normal orientation".
The application operator maps a point from the unit square onto the physical domain taking into account the parameter domain given in the constructor.
Definition at line 66 of file elementMaps3D.hh.
Constructor & Destructor Documentation
◆ MapTetrahedron3d() [1/2]
Constructor. The values of scX, scY and scZ are only for the map, they are not needed by the user for mapping a point from the reference element onto the Real element.
- Parameters
-
map The element map for this tetrehdron as a string, x, y and z are the allowed variables, the component are separated by a comma. scX The range of x is [0, scX]. scY The range of y is [0, scY]. scZ The range of z is [0, scZ].
◆ MapTetrahedron3d() [2/2]
Constructor. Takes the four physical corners of the tetrahedron and computes the element map: 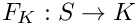
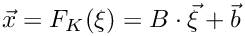
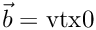
![$B = [ (\mbox{vtx1} - \vec b)
(\mbox{vtx2} - \vec b) (\mbox{vtx3} - \vec b) ]$](form_389.png)
◆ ~MapTetrahedron3d()
|
inline |
Definition at line 91 of file elementMaps3D.hh.
Member Function Documentation
◆ clone()
|
inline |
Returns a copy of the map.
Definition at line 129 of file elementMaps3D.hh.
◆ info()
|
inlinevirtualinherited |
Returns information in an output stream.
Reimplemented from concepts::OutputOperator.
Reimplemented in concepts::MapHexahedron3d, concepts::MappingHexahedron3d, and concepts::PartMappingHexahedron3d.
Definition at line 28 of file elementMaps3D.hh.
◆ jacobian()
|
inline |
Returns the jacobian.
Definition at line 123 of file elementMaps3D.hh.
◆ operator()()
Returns a point in 3D mapped from the unit cube [0,1]3 onto the element in the original mesh.
If the map was given as formula in the constructor, the parameters are directly inserted into the formula. If the map was given by the four corners of the physical tetrahedron, then the point is first mapped from the unit cube ( 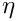
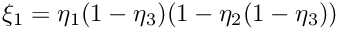
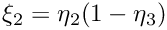
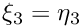
- Returns
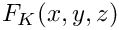
- Parameters
-
x ![$\in [0, 1]$](form_383.png)
y ![$\in [0, 1]$](form_383.png)
z ![$\in [0, 1]$](form_383.png)
Definition at line 109 of file elementMaps3D.hh.
The documentation for this class was generated from the following file:
- geometry/elementMaps3D.hh
Generated on Wed Sep 13 2023 21:06:39 for Concepts by
