bem::AdaptLaplaceSL01< F > Class Template Reference

#include <bformAdapt.hh>

Inheritance diagram for bem::AdaptLaplaceSL01< F >:

Public Member Functions
	AdaptLaplaceSL01 (uint stroud=0, uint gauss=0, concepts::Real deltaI=1.0, concepts::Real dist=0.0, concepts::Real eta=0.5)
void	operator() (const concepts::Element< F > &elmX, const concepts::Element< F > &elmY, concepts::ElementMatrix< F > &em)
void	operator() (const Constant3d001< F > &elmX, const Constant3d001< F > &elmY, concepts::ElementMatrix< F > &em)
virtual AdaptLaplaceSL01 *	clone () const
virtual void	operator() (const Element< G > &elmX, const Element< G > &elmY, ElementMatrix< F > &em) const =0
virtual void	operator() (const Element< G > &elmX, const Element< G > &elmY, ElementMatrix< F > &em, const ElementPair< G > &ep) const

Protected Member Functions
virtual std::ostream &	info (std::ostream &os) const
	Returns information in an output stream.

Detailed Description

template<class F>
class bem::AdaptLaplaceSL01< F >

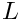
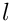
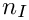
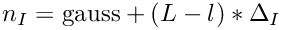
Bilinear form for the Laplace Single Layer potential with piecewise constant shape functions and hanging nodes (=> recursive subdivision of the larger triangle). Number of integration points depends on the level of the element. The number of integration points given in the constructor is used for the highest level . For an element on level the number of integration points in each dimension is given by .

Parameters

F	Field (Real or Cmplx)

Definition at line 263 of file bformAdapt.hh.

Constructor & Destructor Documentation

AdaptLaplaceSL01()

template<class F >

bem::AdaptLaplaceSL01< F >::AdaptLaplaceSL01 ( uint  stroud = 0, uint  gauss = 0, concepts::Real  deltaI = 1.0, concepts::Real  dist = 0.0, concepts::Real  eta = 0.5  )

inline

3-dim quadrature (3-d Gauss)

Parameters

stroud	number of integration points in the integration formula for the outer ($x$) integration.
gauss	number of Gauss points in the integration formula for the inner ($y$) integration and the case where the two panels intersect.
deltaI	Additional number of integration points per level
dist	distance to distinguish between near/far field (far field if the distance between the two centers of the panels is larger than dist => 1-point formular)
eta	ratio between element size and distance for recursive subdivision ( )

Definition at line 343 of file bformAdapt.hh.

Member Function Documentation

clone()

template<class F >

virtual AdaptLaplaceSL01 * bem::AdaptLaplaceSL01< F >::clone ( ) const

inlinevirtual

Virtual constructor. Returns a pointer to a copy of itself. The caller is responsible to destroy this copy.

Implements concepts::BilinearForm< F, G >.

Definition at line 296 of file bformAdapt.hh.

info()

template<class F , class G = typename Realtype<F>::type>

virtual std::ostream & concepts::BilinearForm< F, G >::info ( std::ostream &  os ) const

protectedvirtualinherited

Returns information in an output stream.

Reimplemented from concepts::OutputOperator.

Reimplemented in constraints::ConstraintsList< F >, hp1D::Laplace< F >, hp1D::Identity< F >, hp1D::IdentityParallel< F >, hp1D::BiLaplace< F >, hp1D::Jump1Jump1< F >, hp1D::Mean2Jump1< F >, hp1D::Jump1Mean2< F >, hp2D::Advection< F >, hp2D::Identity< F >, hp2D::Laplace< F >, hp2D::LaplaceMatrix< F >, hp2D::BilinearFormOnePartDeriv< F >, hp2D::BilinearFormTwoPartDeriv< F >, hp2D::DivDiv< Weight >, hp2D::RotRot, hp2Dedge::Graduv< F >, hp2Dedge::GraduvMatrix< F >, hp2Dedge::Identity< F >, hp2Dedge::IdentityMatrix< F >, hp2Dedge::RotRot< F >, hp2Dedge::Rotuv, hp2Dedge::EdgeIdentity, hp3D::LinearElasticity< F >, hp3D::BilinearFormTwoPartDeriv< F >, hp3D::Laplace< F >, hp3D::Identity< F >, hp3D::Advection< F >, hp3D::DivDiv< Weight >, hp3D::Hook, hp3D::RotRot, concepts::BilinearFormLiCo< F, G >, concepts::BilinearFormContainer< F, G >, concepts::BilinearFormContainer< F, typename Realtype< F >::type >, concepts::BilinearFormContainer< Real, Real >, concepts::BilinearF_Sum< F, H, J, G >, concepts::BilinearF_W< F, H, J, G >, and vectorial::BilinearForm< F, G >.

operator()() [1/3]

template<class F >

void bem::AdaptLaplaceSL01< F >::operator()	(	const concepts::Element< F > &	elmX,
		const concepts::Element< F > &	elmY,
		concepts::ElementMatrix< F > &	em
	)

Application operator.

Exceptions

MissingFeature

Parameters

elmX	Element
elmY	Element
em	Element matrix for the two given elements.

operator()() [2/3]

template<class F , class G = typename Realtype<F>::type>

virtual void concepts::BilinearForm< F, G >::operator() ( const Element< G > &  elmX, const Element< G > &  elmY, ElementMatrix< F > &  em  ) const

pure virtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element (test functions)
elmY	Right element (trial functions)
em	Return element matrix

Implemented in vectorial::BilinearForm< F, G >, concepts::BilinearFormLiCo< F, G >, concepts::BilinearFormContainer< F, G >, concepts::BilinearF_Sum< F, H, J, G >, and concepts::BilinearF_W< F, H, J, G >.

operator()() [3/3]

template<class F , class G = typename Realtype<F>::type>

virtual void concepts::BilinearForm< F, G >::operator() ( const Element< G > &  elmX, const Element< G > &  elmY, ElementMatrix< F > &  em, const ElementPair< G > &  ep  ) const

inlinevirtualinherited

Evaluates the bilinear form for all shape functions on elmX and elmY and stores the result in the matrix em. If this method is not reimplemented in a derived class, the default behaviour is to call the application operator without ep.

Postcondition

The returned matrix em has the correct size.

Parameters

elmX	Left element
elmY	Right element
em	Return element matrix
ep	Element pair holding more information on the pair elmX and elmY

Reimplemented in vectorial::BilinearForm< F, G >.

Definition at line 57 of file bilinearForm.hh.

---

The documentation for this class was generated from the following file:

• bem/bformAdapt.hh